拉马努金：预见黑洞的印度数学先知，直觉超越时代的传奇

一个未尝大学殿堂的普通职员，凭借着近乎偏执的直觉，独立发现了数千个深奥的数学定理。更令人惊奇的是，在他去世近百年后，他那些看似疯癫的笔记，竟然成为了我们理解黑洞和弦理论的关键钥匙。这听起来是否有些不可思议？

今天，我们将深入探讨这位传奇人物——斯里尼瓦瑟·拉马努金的故事。他的生平不仅是一个天才陨落的悲剧，更是一部融合了直觉、信仰、文化冲突乃至人类智力极限的宏大史诗。一位被贫困和疾病缠绕的印度数学先知，如何在他的精神世界中触碰无限，甚至预见了未来世界的物理学结构？

贫瘠土壤中的天才萌芽

想象一下1887年的印度南部小镇库姆巴科南，那是一个极端贫困的年代。在这样的环境下，拉马努金诞生了。他的父亲仅是一名微薄收入的布店小职员，勉强维持生计。然而，他的母亲，一位虔诚的婆罗门女性，却将深厚的宗教信仰和坚韧的意志融入了他的灵魂，这成为了他一生中最重要的精神支柱。

拉马努金的数学天赋发展得异常之早，甚至到了“反常”的地步。十岁时，他在学校表现优异，但对数学的痴迷已达到偏执的程度。十二岁那年，他已经自学完大学高级三角学，甚至独立推导出了欧拉公式 ($e$ 的 $i\pi$ 次方等于负一)。当他得知这个公式早已存在时，竟然感到了失落。试想一个孩子，他对 “零除以零” 这样的哲学问题念念不忘，这绝非寻常儿童所能。他并非被传统的算术规则所束缚，而是凭借直觉，直接触碰到了极限与无穷的边缘。

神秘“天书”与直觉的崛起

真正改变拉马努金命运的，是十五岁时偶然得到的一本名为《纯粹数学基本结果概要》的书。这本书并非传统教材，更像是一本备考手册，里面罗列了大约五千个定理和公式，却几乎不提供证明。对普通学生而言，这无疑是本 “天书”，只能死记硬背。但对拉马努金而言，这仿佛是一本来自外星文明的“解密手册”，充满了等待他破译的密码。

拉马努金的独特性在于，他被迫建立起自己独特的符号系统，发展出一套基于直觉、归纳和类比的 “验证” 方法。他跳过了欧洲数学界几个世纪建立的严格演绎推理体系，直接 “看到了” 结论。

这种独特的自学经历带来深远影响：拉马努金并不区分什么是“基础”数学，什么是“前沿”数学。卡尔那本书中涉及的连分数、超几何级数和伯努利数，正是他后来成为一代宗师的领域，这或许是命运的安排。

现实困境与数学孤旅

1904年，拉马努金凭借数学天赋获得奖学金，进入库姆巴科南政府学院。然而，天才往往是孤独的，甚至有些 “格格不入”。他对数学的痴迷达到了病态程度，上英语课、历史课时都在草稿纸上演算。结果是灾难性的——所有非数学科目全部挂科，奖学金也被取消。

这对他造成巨大打击，他曾离家出走，甚至被当地报纸报道为 “失踪的男孩”。他试图在其他学院继续学业，结果如出一辙：数学满分，其他科目不及格。到1907年，他彻底放弃了学位追求，这意味着失去了所有 “正常” 的职业道路。

从1907年到1912年，拉马努金度过人生中最 “荒野” 的岁月。没有正式工作，没有稳定收入，仅靠朋友接济和家教谋生。在极度贫困中，他将所有精力投入数学研究。因纸张昂贵，他甚至习惯在石板上演算，只将最终结果抄录到笔记本上。

这些笔记本后来成为数学史上的传奇。现存的拉马努金三本笔记本中，涵盖约三千到四千个公式，涉及素数分布、无穷级数、模方程等。这些公式每一个都是等待挖掘的宝藏，却没有任何证明。哈代后来耗费大量时间验证，结果无一例外，全部精准无误。

跨越山海的数学之约

1909年，在家人的安排下，拉马努金娶了年仅九岁的贾纳基为妻。婚姻让他不得不面对现实**：养家糊口**。他开始拿着破旧的笔记本，拜访马德拉斯的数学爱好者。印度数学学会创始人拉马斯瓦米·艾耶尔一眼识出他的非凡，认为让这样一位天才去税务局当小职员无疑是暴殄天物，建议他去见同样热爱数学的税收官R. 拉马钱德拉·拉奥。

拉奥起初不信，以为拉马努金是抄袭者。但在拉马努金深入解释了椭圆积分的复杂性后，拉奥彻底被征服，同意资助他的研究。然而，拉马努金不愿长期接受慈善。1912年，他在马德拉斯港务局找到一份会计职员的工作。这份工作成为他与西方数学界接轨的关键跳板——他的上司S. 纳拉亚纳·艾耶尔和主席弗朗西斯·斯普林爵士都懂数学，他们不仅允许拉马努金在闲暇时研究数学，更鼓励他将成果寄给英国的数学家。

于是，戏剧性的一幕发生了。我们现在都知道，那封1913年1月16日，寄往英国剑桥大学的信，彻底改变了拉马努金的命运，也改写了数学史。

在此之前，拉马努金也尝试联系其他英国数学家，但都石沉大海。伦敦大学学院的教授希尔回信，却表示无法理解。而剑桥的两位数学巨擘——霍布森和贝克，甚至懒得回复。在当时的英国学术界看来，一个没有学位的印度职员寄来的信，里面充满奇怪符号，很容易被视为 “民间科学家” 的胡言乱语。

但这封寄给G.H. 哈代的信，彻底不同了。信的开头，拉马努金写得非常谦卑，甚至有些卑微：

“尊敬的先生，以此信冒昧打扰……我是马德拉斯港务局账务部的一名职员，年薪仅二十英镑……”但他随信附上的九页纸，却包含了大约一百二十个数学公式，涉及定积分、椭圆函数、数论等领域。

哈代收到信的第一反应也是怀疑。他看到关于素数分布的公式，有些似曾相识，有些闻所未闻。但当晚，他和长期合作者约翰·利特尔伍德在三一学院的房间里仔细审查这些公式后，他们的态度发生了一百八十度的大转变。哈代后来形容，这些公式 “完全打败了我”，他断定它们一定是真的。“没有人会有如此丰富的想象力去编造它们，如果是骗子，他必须比数学天才更天才。”

哈代立刻回信，热情邀请拉马努金前往剑桥。然而，事情并非一帆风顺。作为一名正统婆罗门，跨越海洋在当时的印度社会被视为严重禁忌，意味着失去种姓地位。拉马努金一开始以宗教原因拒绝了邀请，这让哈代非常失望。

转机来自两方面。首先是剑桥数学家内维尔受哈代之托，亲自到马德拉斯游说拉马努金。但更关键的，是拉马努金内心的信仰。据说，他的母亲做了一个梦，梦见家族女神娜玛吉里警告她不要阻碍儿子的前程。而拉马努金自己也声称，他得到了女神的许可。

就这样，1914年3月17日，拉马努金剪掉了象征婆罗门身份的发髻，告别妻子和母亲，登上了 “涅瓦萨号” 邮轮，驶向了寒冷而陌生的英国。这不仅是他一个人的旅程，更是两种文明、两种思维方式的跨越式碰撞。

剑桥岁月：直觉与严谨的交锋

抵达剑桥后，拉马努金住进了三一学院。哈代尽力照顾，但拉马努金面临巨大的文化和生活挑战。他是一位严格的素食主义者，在第一次世界大战期间的英国，寻找合适的素食异常困难。他无法适应学院食堂的饮食，经常只能在房间里自己煮饭。缺乏新鲜蔬菜水果，加上英国阴冷潮湿的气候，他的健康状况开始出现隐患。

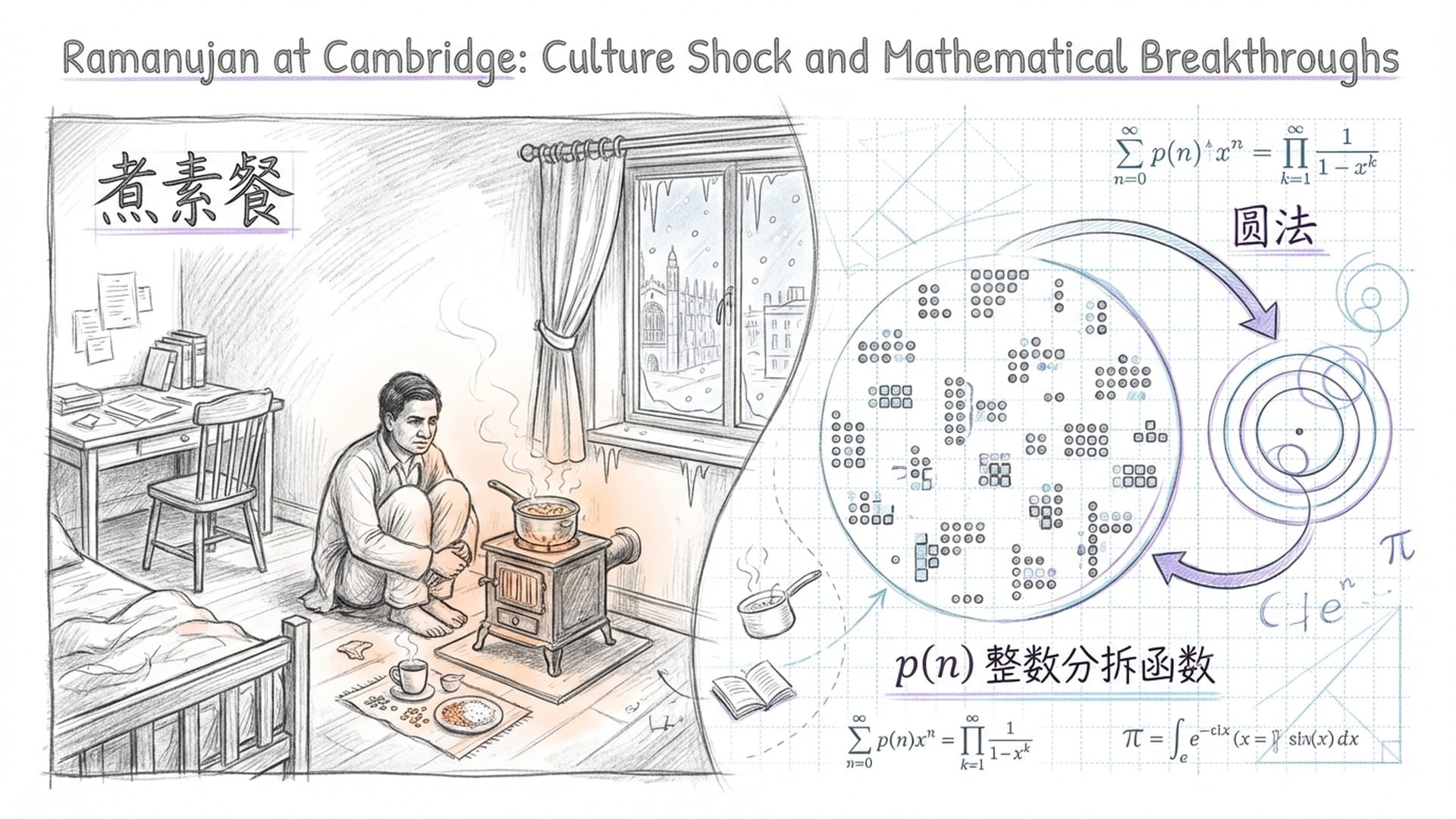
更深层的冲突发生在学术层面。哈代面临一项微妙的任务：他必须教会拉马努金现代欧洲数学的 “严格证明”，但又不能破坏他那宝贵的 “直觉”。这是一个关于两种截然不同知识体系如何对话的故事。拉马努金习惯通过直觉跳跃至结论，而哈代则坚持每一步都必须有逻辑支撑。哈代后来将这段合作描述为他生命中 “唯一的浪漫事件”，其中包含了多少欣喜、无奈与来之不易。

在剑桥期间，两人合作产生了多个里程碑式的成果，其中最著名的便是对 “整数分拆函数” 的研究。

什么是整数分拆？即将一个正整数表示成若干个正整数之和的方法数。例如，四可以分成四，或者三加一，或者二加二，或者二加一加一，或者一加一加一加一。因此 $p(4)$ 等于五。对于小数字这很容易，但 $p(200)$ 却大约是 $3.9 \times 10^{12}$。当时的数学界普遍认为，根本不可能找到一个精确公式来描述 $p(n)$ 的增长。

但拉马努金凭借他对数字的深刻洞察，提出了一个惊人的渐近公式。为证明这个公式，哈代和拉马努金发明了一种前所未有的方法——“圆法”。

圆法的核心思想是利用生成函数的柯西积分公式。他们构造一个以原点为中心的圆上的围道积分，然后将圆周划分为 “优弧” 和 “劣弧”。优弧，即在某些有理点附近，函数值起主导作用。这是拉马努金直觉的核心——他知道在这个圆周上，有些点就是比其他点 “更重要”。而劣弧呢，在其他区域，函数值相对较小，可作为误差项处理。

这种方法不仅解决了整数分拆问题，更成为解析数论中最强大的工具之一，后来被哈代和利特尔伍德进一步完善，用于解决华林问题和哥德巴赫猜想等。这就像他们开创了一个全新的维度，以一种从未有人想过的方式，去攻克看似无法解决的难题。

数字的先知与跨越时空的预言

在剑桥的最后岁月里，拉马努金病重住院。哈代前去探望他时，随口提到自己坐的出租车牌号是 一七二九，觉得这数字 “沉闷” 又 “不祥”。拉马努金躺在病床上，立刻反驳：“不，哈代，这是一个非常有趣的数字！它是可以用两种不同方式表示为两个立方之和的最小正整数。”

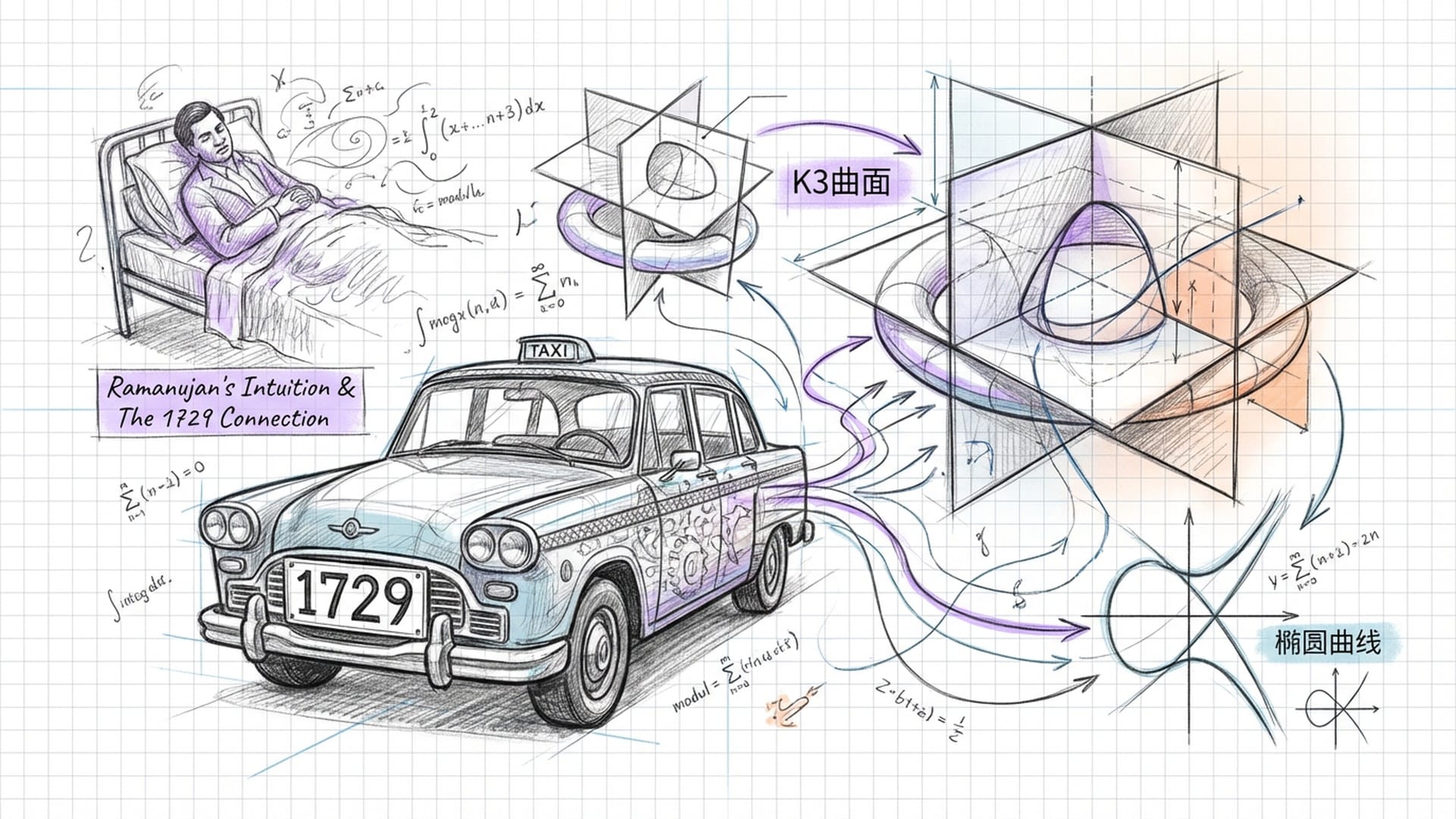
你知道吗？1729 等于 1³ + 12³，也等于 9³ + 10³。这个轶事，不仅展示了拉马努金对数字惊人的敏感度，也揭示了他对特定数学结构（如椭圆曲线和K三曲面）的直觉。现代研究表明，拉马努金对这类数字的研究，实际上触及了几十年后才被命名的K三曲面的性质。这种深层几何结构，直到二十世纪下半叶才被代数几何学家完全理解。拉马努金在没有任何现代代数几何工具的情况下，凭借纯粹的算术直觉，“看到” 了这些结构。他就像一位盲眼先知，提前触摸到了未来世界的脉络。

还有罗杰斯-拉马努金恒等式，这是两个涉及基本超几何级数的恒等式，连接了无限级数和无限乘积。拉马努金在1913年之前就发现了它们，同样没有给出证明。这些恒等式后来被赋予深刻的组合数学含义，甚至在统计力学和共形场论中，找到了惊人的物理应用。

命运的玩笑：误诊与绝笔

从1917年开始，拉马努金的健康状况急剧恶化。他被诊断为肺结核，在当时几乎是绝症。他被迫辗转于多家疗养院，不仅要忍受身体的痛苦，还要面对更加严格的饮食限制和与世隔绝的孤独。

这种身心双重折磨使他陷入严重抑郁。1918年初，他在伦敦地铁站试图跳轨自杀，所幸列车员及时发现并紧急制动，他虽重伤但保住性命。当时在英国，试图自杀是重罪，拉马努金一度面临被捕风险。最终是哈代利用其影响力，才使警方撤销了指控。这一事件揭示了这位天才辉煌成就背后，隐藏着多么巨大的心理深渊。

然而，在病痛折磨之下，数学成就却获得了最高级别的认可。1918年5月，在哈代等人的极力推荐下，拉马努金被选为英国皇家学会会员。这是英国科学界的最高荣誉。他不仅是历史上第二位获此殊荣的印度人，而且年仅三十一岁，是最年轻的会员之一。紧接着，10月，他又被选为剑桥三一学院的研究员，是该学院历史上的首位印度人。这些荣誉不仅带来了每年二百五十英镑的津贴，解决了他的经济后顾之忧，更重要的是，极大地鼓舞了他的精神，使他的病情一度出现好转迹象。

1919年，随着一战结束，海路畅通，拉马努金决定返回印度养病。然而，回国后，他的病情并未如预期般好转，反而在一年后恶化并去世了。

长期以来，传记和历史记录都将拉马努金的死因归结为肺结核。然而，1994年，英国医生D.A.B. 杨对拉马努金当年的医疗记录和症状进行了详尽的现代医学分析，提出了一个颠覆性结论：拉马努金很可能并非死于肺结核，而是死于肝阿米巴病。

杨医生给出了证据：拉马努金在离开印度前曾患过严重的痢疾，这是阿米巴感染的典型前兆。如果不彻底治疗，阿米巴原虫可在体内潜伏多年，最终侵入肝脏导致脓肿。他在英国期间表现出的症状，如反复发烧，对某种治疗的反应，都更符合阿米巴病而非典型的肺结核。最令人痛心的是，如果当时的医生能正确诊断出来，阿米巴病在当时已是完全可以治愈的。这次误诊，加上战时英国匮乏的素食供应导致的严重维生素缺乏，最终导致了悲剧的发生。

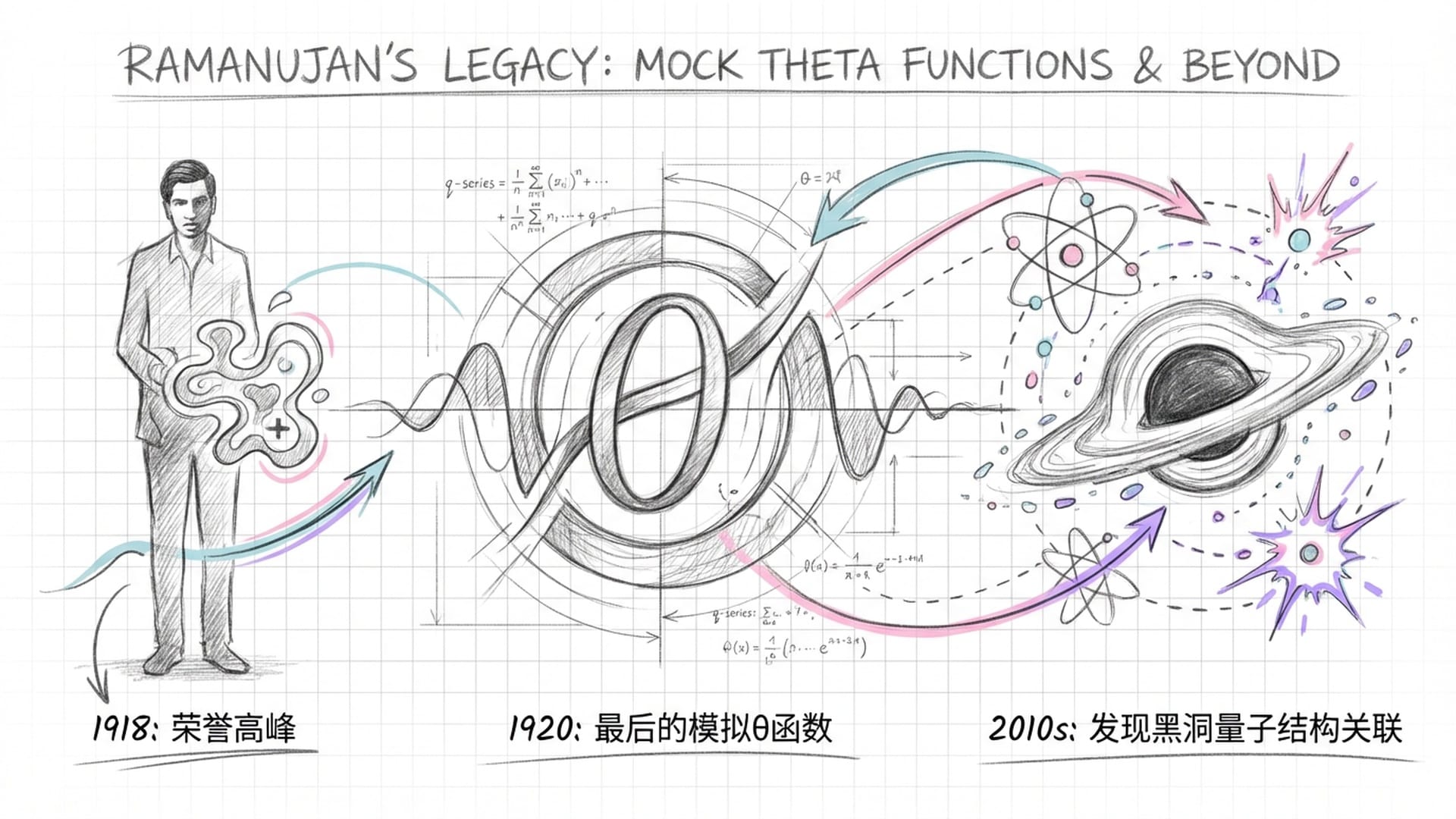
回到印度后，尽管身体极度虚弱，甚至难以握笔，拉马努金的数学创造力却达到了前所未有的顶峰。他在给哈代的最后一封信中，提出了一个全新的、也是他最后的主要数学贡献——“模拟θ函数”。他在信中写道：

“我发现了一些非常有趣的函数……它们像θ函数一样，但在某些方面又完全不同。”

他列出了十七个这样的函数，并将其分为三阶、五阶和七阶。哈代虽然无法完全理解这些函数的全貌，但他凭借直觉意识到这是非常重要的工作，并在拉马努金去世后将其发表。

1920年4月26日，斯里尼瓦瑟·拉马努金在马德拉斯总统管辖区的库姆巴科南逝世，年仅三十二岁。

尘封的宝藏与未来的回响

拉马努金去世后，他的遗孀贾纳基整理了他的遗物，包括最后一年在印度写下的散乱手稿。这些手稿后来被寄给了哈代，并在哈代去世后辗转到了G.N. 沃森手中。沃森曾打算整理这些手稿，但未能完成。随后，这些无价之宝被存放在剑桥大学三一学院雷恩图书馆的一个盒子里，并被世界遗忘了半个世纪。想象一下，人类的瑰宝，就那么静静地躺在角落里，等待被发现。

直到1976年春，美国宾夕法尼亚州立大学的数学家乔治·安德鲁斯访问三一学院图书馆。在翻阅沃森的遗物时，他意外发现了一叠大约一百三十八页的散乱手稿。安德鲁斯立刻认出这是拉马努金独特的笔迹。这就是后来轰动数学界的 “遗失的笔记本”。

这本笔记包含了六百多个没有任何证明的公式，主要集中在 q-级数 和拉马努金临终前发现的模拟θ函数上。这一发现被比作数学界的 “贝多芬第十交响曲” 的出土。

但最令人震惊的转折，发生在二十一世纪。随着弦理论的发展，物理学家在研究黑洞熵时，遭遇了数学障碍。他们需要计算黑洞事件视界上的量子微观状态数。

2010年代，肯·小野等数学家和物理学家发现，拉马努金在1920年凭直觉发现的模拟θ函数，竟然是描述这些黑洞量子结构的理想数学工具。具体来说，模拟θ函数的模形式性质，正好对应了全息原理中引力与量子场论的对偶关系。拉马努金在完全没有任何量子力学知识背景的情况下（量子力学在他去世后才真正建立），提前近一个世纪预见到了描述宇宙最神秘天体所需的数学结构。这简直是穿越时空的预言！他就像一个未卜先知的魔法师，在没有任何现代设备的情况下，看到了未来世界的运行法则。

默默守护的记忆与不朽传奇

在拉马努金的故事中，我们往往容易忽略他年轻的妻子贾纳基。她在拉马努金去世后孀居长达七十四年，直到1994年以九十五岁高龄去世。

在这漫长的岁月里，她生活简朴，靠微薄的养老金度日。她后来收养了一个儿子，并致力于保存拉马努金的记忆。她经常接待来自世界各地的数学家，虽然她完全不懂数学，但总是自豪地分享关于丈夫的回忆。她曾对访客说，她记忆中的拉马努金 “总是被数字和算式包围，除了数学，他对世界一无所知”。她的存在，成了连接那个传奇时代与现代世界的活化石，默默守护着一段伟大的记忆。

拉马努金的故事，因其戏剧性——天才、贫穷、跨文化友谊、早逝——而成为了流行文化的宠儿。例如，罗伯特·卡尼格尔的传记《知无涯者》，将拉马努金介绍给了大众。2015年改编的同名电影，由戴夫·帕特尔饰演拉马努金，杰瑞米·艾恩斯饰演哈代，生动再现了两人在剑桥的合作与冲突。还有Complicite剧团的戏剧《消失的数字》，不仅讲述了他们的故事，还深入探讨了数学中的无穷概念与人类存在之间的哲学联系，获得极高评价。

斯里尼瓦瑟·拉马努金的一生，是对人类智力极限的一次壮丽探索。他证明了知识的获取不仅可以通过严密的逻辑推理，也可以通过深邃的直觉洞察。他与哈代的合作，留下了关于东西方文化碰撞与融合的永恒启示：当严谨的证明体系遇上狂野的直觉天赋，并未发生毁灭性的冲突，反而共同构建了通往真理的阶梯。

在他逝世一百多年后的今天，从数论的深处到黑洞的边缘，拉马努金的思想依然在回响。他是一个真正 “知道无限” 的人，而通过他，我们也得以窥见无限的一角。