颠覆你的“常识”：为什么世界不是“平均主义”的？一文读懂“幂律分布”的底层逻辑

颠覆常识：你以为的公平，可能只是个美丽的谎言

你是否曾怀疑过，我们习以为常的“公平”和“平均”是否只是构建了我们心灵的舒适区？今天，我们将揭示一个可能颠覆你世界观的底层逻辑——幂律分布。它并非遥不可及的学术概念，而是深刻影响我们日常生活、职业发展乃至投资决策的底层规律。

正态分布的“假象”与世界的“狂野西部”

我们从小接受的教育，总是围绕着正态分布展开。身高、智商、考试成绩，大部分人聚集在“平均线”附近，少数人出类拔萃，少数人垫底。这种钟形曲线模型，构建了我们对“多劳多得”、“中庸之道”的朴素认知，给人一种只要努力就能达到平均水平的安全感。

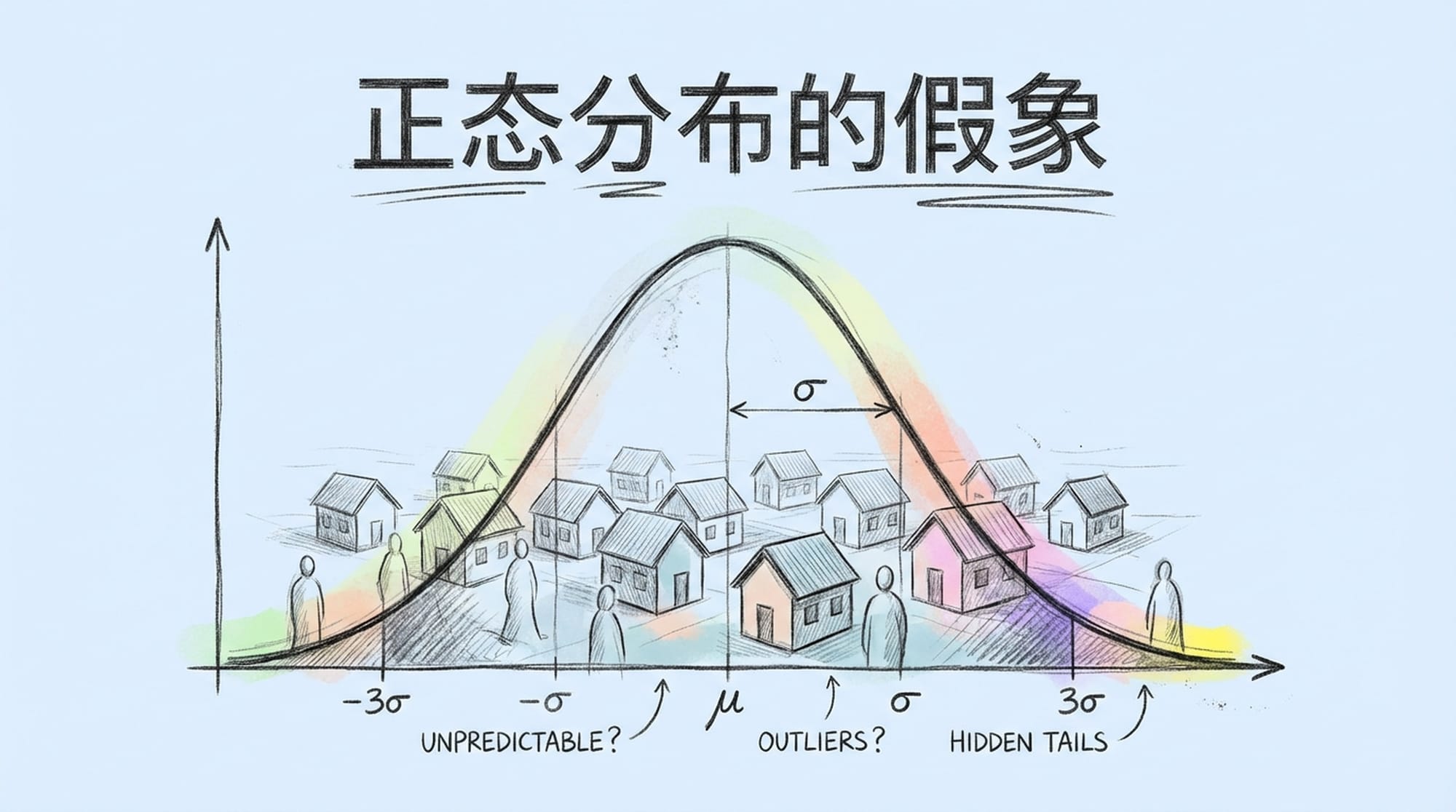
然而，真实世界远比理想化的正态分布来得复杂和“狂野”。

这个世界，它根本不是一个规规矩矩的钟形曲线。它更像是一个无序的、充斥着极端事件的“狂野西部”。

在这里，一小撮人攫取了绝大部分财富，少数视频贡献了绝大多数播放量，少数公司占据了大部分市场利润。这听起来似乎不那么“公平”，甚至让人心生不满。但请先别急着抱怨，这很可能并非某种刻意为之的“不公”，而是这个世界运行的底层游戏规则。

帕累托的惊人发现：财富分配的“长尾巴”

一百多年前，意大利工程师维尔弗雷多·帕累托（Vilfredo Pareto）偶然涉足了财富分配研究。他仔细查阅了意大利、英国、法国等国的税收记录，绘制出收入数据图，结果发现了一个惊人的事实：无论哪个国家，财富的分配都呈现出相似的模式。这不是一个钟形曲线，而是一条拖着长长尾巴的曲线。

大部分人收入低下，但曲线突然变得平缓，这意味着有那么一小撮人，他们赚的钱是普通人的好几倍、几十倍，甚至几百倍！这在正态分布里根本不可能的事儿，它真实地发生了。

这种分布模式揭示了财富分配的极端不平衡现状，即我们常说的“二八定律”的雏形。

幂律：残酷而真实的“无声判决”

为了更好地理解这种现象，帕累托对数据进行了对数转换。奇迹出现了！那条原本弯弯曲曲的“长尾巴”曲线，竟然变成了一条笔直的直线。

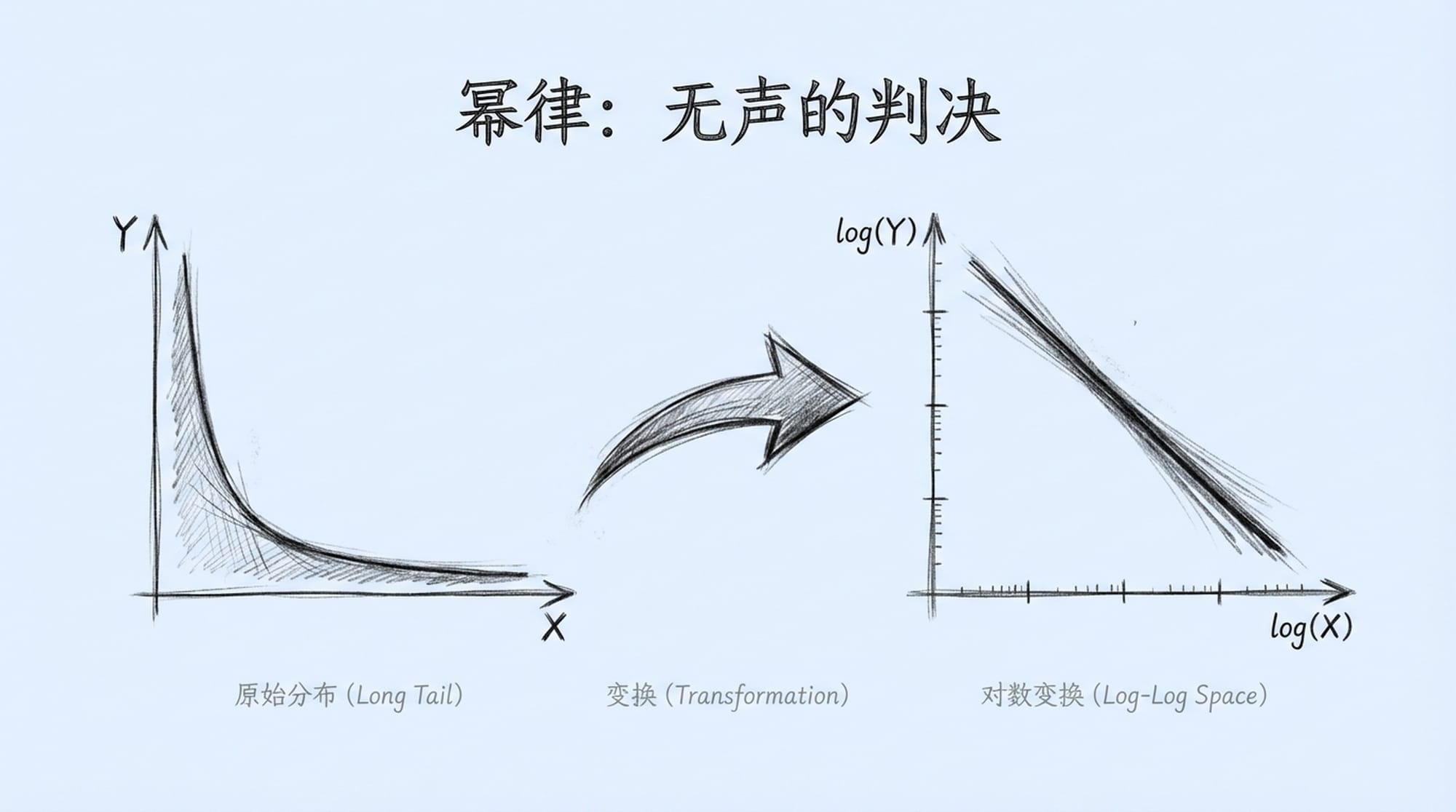
这条直线揭示了一个残忍的真相：当收入每翻一倍，能达到这个收入的人数就会以一个固定的比例迅速下降。这意味着你赚得越多，与你处于同等财富水平的人就越少。这就是幂律，它犹如一道无声的判决，无情地宣告着这个世界马太效应的普遍性。

玩转“分布游戏”：理解不同规则下的世界

为了让你更直观地理解正态分布与幂律分布的差异，我们来玩三个“小游戏”。

游戏一：加法效应的“老好人”

想象一个简单的掷硬币游戏：你投掷一百次硬币，每次正面朝上你就赢一美元。

• 结果：你的期望收益是五十美元，无论玩多少次，结果大体上都在五十美元附近波动。
• 特点：每个硬币的微小波动都能被其他硬币**“中和”**。
• 启示：这便是正态分布。它是一个“老好人”，喜欢将所有事情拉回到平均线上。身高、体温等无数相互独立且叠加的随机变量，最终都会趋向正态分布。它给人一种**“只要努力，就能达到平均线”**的错觉。

游戏二：乘法效应的“心机婊”

现在改变规则：你初始拥有一美元，每次投掷硬币。正面朝上，你的钱乘以 1.1；反面朝上，你的钱乘以 0.9。投掷一百次后，你的钱会变成多少？

• 结果：尽管每次翻面的期望倍数看似是 1，但实际情况却异常惨烈。连续一百次反面可能让你只剩几分钱；而连续一百次正面则可能让你获得近一万四千美元！这个游戏的中位数大约只有 0.3 美分，意味着绝大多数人都输得精光，只有极少数人赚得盆满钵满。
• 特点：这是乘法效应的体现，它导致了对数正态分布。
• 启示：股市波动、投资回报率、公司的快速增长，往往都是乘法效应的结果。它告诉你，财富积累并非简单叠加，**“黑天鹅事件”**既可能让你血本无归，也可能让少数幸运儿财富暴涨。

游戏三：纯粹幂律的“大魔王”

最后一个游戏更加刺激，它被称为**“圣彼得堡悖论”**：你初始拥有一美元。每次投掷硬币，正面朝上游戏结束，你可以拿走 2 的 N 次方美元（N是你投出正面为止的次数）。

• 结果：第一次正面，你拿走 2 美元；第二次正面，你拿走 4 美元；第三次正面，你拿走 8 美元……这个游戏的期望收益理论上是无限的！
• 特点：尽管连续多次才出现正面的概率很小，但一旦发生，回报却是指数级爆炸。
• 启示：这种纯粹的幂律分布最可怕的一点是，它没有“宽度”，或者说，它的标准差是无限的。这意味着我们平时熟悉的“平均值”概念，在幂律世界里形同虚设，因为它会被极少数的极端事件彻底“扭曲”。

你测量的数据越多，其平均值反而可能越大！这就好比你走进一间屋子，里面有九十九个身家百万的人，平均身家看起来很高。但若此时马云和王健林也走了进来，你再计算平均值，会发现它已经被这两个“极端值”拉升到了一个你认知以外的维度。

幂律世界的本质：少数“异类”的决定性力量

在幂律分布的世界里，那些“平均的”、“差不多的”事物根本不重要。真正具有决定性影响力的是那些极少数的“异类”，那些**“黑天鹅”，那些“颠覆者”**。

那么，幂律分布究竟是如何产生的？它通常是**两个指数效应“共舞”**的结果。例如，在圣彼得堡悖论中，你赢钱的金额是指数级增长的，但你赢得大笔钱的概率却是指数级衰减的。两者碰撞，便形成了幂律。

在自然界中，地震就是一个典型例子。小地震频繁发生，但破坏力有限，其频率随震级增大呈指数级下降。然而，地震的破坏力（释放的能量）却随震级呈指数级增长。这“两个指数”一结合，便发现地震能量的释放也遵循幂律分布。

临界状态与自组织临界性：微小扰动引发“大海啸”

更深层次的原因在于，幂律往往揭示了一个系统处于**“临界状态”。以磁铁为例，当它被加热到居里温度时，磁性会消失。但在即将失去磁性又未完全失去的“临界点”，磁场分布会呈现出“分形”特征**，即无论放大多少倍，其结构都相似，没有固定“尺度”。此时，磁铁内部一个微小的磁力波动，都可能瞬间影响到整个大磁铁！整个系统处于极度不稳定、易变且无法预测的状态，一个微小变化便可能引发**“大海啸”**。

更令人惊叹的是，有些系统甚至不需要外部调节，就能自行演进到“临界状态”，这便是**“自组织临界性”**。

森林火灾是绝佳的例证。小火灾屡见不鲜，大火灾不时发生。研究发现，森林火灾的面积分布也遵循幂律：小火多，大火少，但少数大火却能烧毁绝大部分面积。当森林茂密到一定程度时，一个平时无关紧要的小闪电，就可能引发一场横扫整个森林的巨型火灾！随后森林变稀疏，重新生长，再次达到“临界点”，周而复始。黄石公园的大火，可能并非特殊事件，而是森林达到临界点后的“自我释放”。地震和沙堆的沙崩也遵循类似规律。

颠覆认知：风险、投资与创新

理解幂律分布对我们而言至关重要，因为它颠覆了我们对风险的认知。

• 在幂律世界里，大多数事件都是“小打小闹”，会给人一种虚假的安全感。你每年都经历小洪水，便觉得洪水不过如此。但几年甚至几十年一遇的“百年一遇”大洪水，却可能瞬间毁灭一切。保险公司若对幂律认知不足，也可能在大灾难面前破产。
• 它也颠覆了我们对投资和创新的理解。为何风险投资公司（VC）大部分项目都失败了，却依然能赚大钱？因为他们投入了那么一两个**“独角兽”**项目！这少数独角兽带来的回报，可能远超所有失败项目造成的损失。

再看更直观的例子：

• 奈飞（Netflix）上，大部分节目都很普通，但几部热门剧占据了绝大部分播放时间。
• YouTube上，你随手上传的视频可能无人问津，但不到百分之四的视频，却贡献了百分之九十三的播放量！这就是幂律的强大威力。

破局之道：拥抱不确定性与寻找极端值

在幂律分布的世界里，你不能指望“雨露均沾”，更不能期望“多劳多得”在你身上处处显灵。你必须清醒地认识到：大多数时候，你都只是那个“平均之下”的大多数。

若想脱颖而出，你必须主动去寻找并把握那些极少数的、可能带来指数级回报的机会。你不能仅仅追求“一致性”，而要拥有**“持久性”，敢于进行几次“赌博”**，并祈祷其中一次能够大获成功。

朋友们，别再被“平均水平”这三个字给PUA了。你可能已经非常努力，但仍在平均线以下挣扎。这并非你不努力，也并非你不够好，而是这个世界的底层逻辑，它从一开始就不是平均主义的。

这也解释了为何世界充满了不确定性。我们的世界在许多地方都处于临界状态。你和朋友做了同样的事情，他可能瞬间爆红，你却波澜不惊。你在工作中提出一个微小建议，可能被忽略，也可能因为某个偶然契机，被领导看中，彻底改变项目走向。我们无法预测哪一块多米诺骨牌会引发雪崩，但雪崩迟早会发生。

那些罕见的、超乎寻常的事件，那些你曾认为“不可能发生”的事情，才是塑造我们世界的真正力量。理解这一点，然后去适应它，去拥抱这种不确定性，甚至去利用这种不确定性，你才能在这个充满复杂性和未知的世界里，找到属于自己的破局之道。

因为，在这个“幂律”的世界里，平均值不是你的方向，极端值，才是英雄的印记。