The 6.7% Secret: DeepSeek AI's Manifold-Constrained Hyper-Connections Revolutionize LLM Training

The 6.7% Secret: Unlocking AI's Next Architectural Revolution

For the past decade, a single, elegant solution has been the bedrock of deep learning: the residual connection. This architectural marvel, ubiquitous in everything from ResNet to the Transformer models powering today's large language models (LLMs), has served as a crucial "information highway" within AI brains. It allows raw data to flow seamlessly, enabling gradients—the signals networks use to learn—to propagate deeply without vanishing.

However, as AI models balloon into trillion-parameter behemoths, this once-super-efficient single lane is showing signs of strain. It's becoming an information bottleneck, threatening to stall the AI revolution.

The Promise and Peril of Hyper-Connections

Imagine widening this critical highway, not just by adding a single lane, but by creating multiple, parallel streams—a multi-lane super-network capable of handling exponentially more data. This is the tantalizing promise of Hyper-Connections (HC). Intuitively, more pathways should mean more expressive power and richer information flow.

"What if we could widen that highway? Not just add another lane, but create multiple, parallel streams—a multi-lane super-network capable of handling exponentially more data? This isn't just a theoretical musing anymore. This is the promise of Hyper-Connections, or HC."

Yet, the reality has been harsh. When researchers attempted to implement these widened highways, they often encountered severe instability during training. It was akin to building a magnificent bridge only for its structural integrity to vanish, causing the entire system to crash.

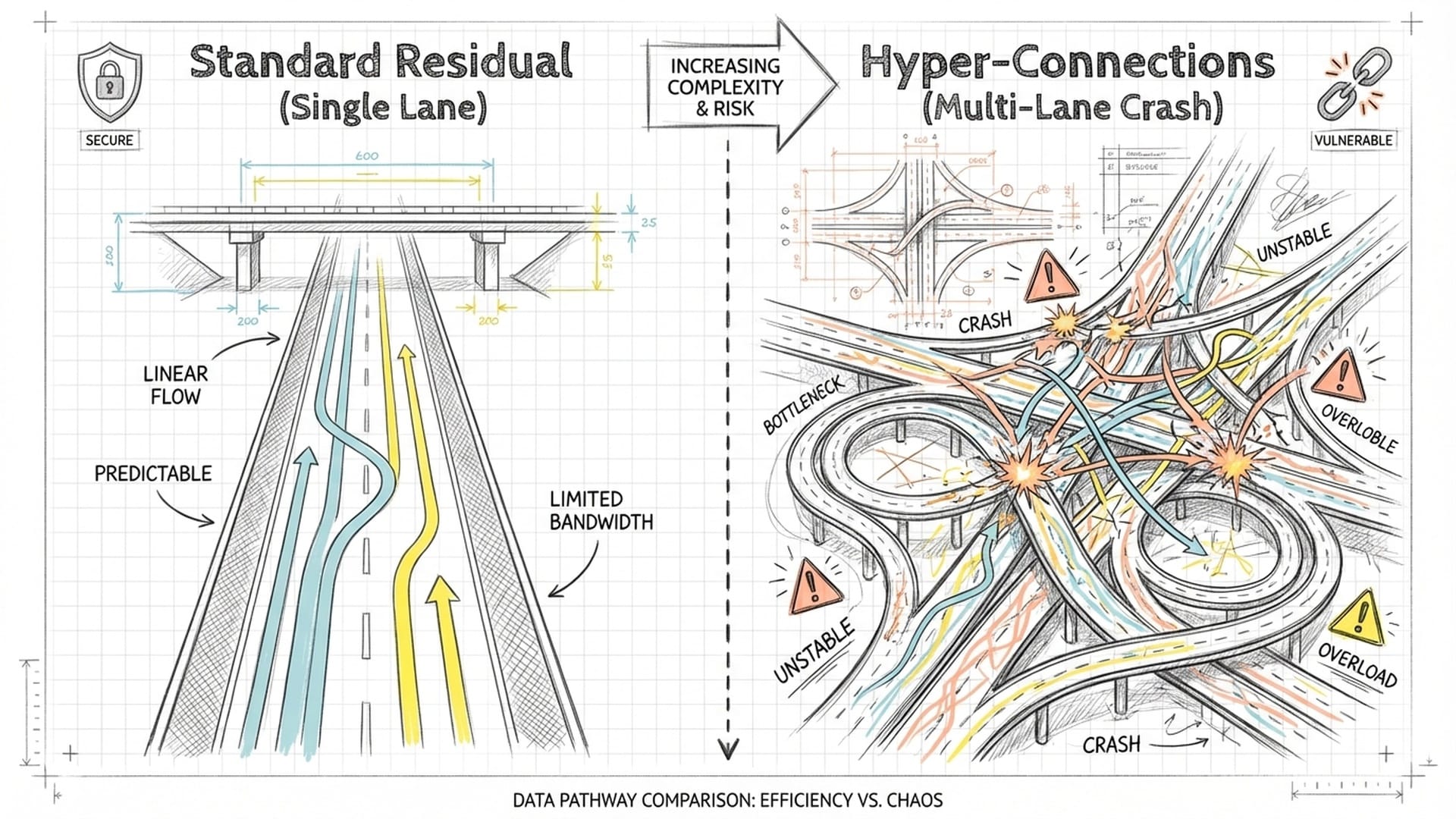
DeepSeek AI's Breakthrough: Manifold-Constrained Hyper-Connections (mHC)

Enter DeepSeek AI, a name that is rapidly gaining prominence. They've unveiled a groundbreaking solution: Manifold-Constrained Hyper-Connections (mHC). This isn't a mere patch; it's a fundamental reinvention, seamlessly blending abstract mathematics with hardcore system engineering to solve this critical stability problem. DeepSeek has not only managed to expand the AI's information highway but has done so in a stable, predictable manner, all with a remarkably low 6.7% additional training overhead.

"This is a ground-up reinvention, bridging the gap from abstract mathematics to hardcore system engineering, all to solve this critical problem. They’ve managed to expand the highway, add those crucial extra lanes, and make it stable. And they’ve done it with a mere 6.7% additional training overhead."

This begs the question: How can one achieve the benefits of a super-wide information highway without the catastrophic stability issues? The answer lies in placing the right guardrails deep within the network's mathematical structure.

The Mathematical Elegance: Birkhoff Polytopes and Doubly Stochastic Matrices

DeepSeek's innovation hinges on projecting the often wild and unconstrained residual mixing matrices onto a very specific, elegant geometric shape: the Birkhoff Polytope, composed of Doubly Stochastic Matrices.

While the terminology may sound complex, the core idea is straightforward: they've discovered a mathematical method to ensure that this widened information highway remains smooth, predictable, and prevents AI models from careening off a cliff.

A doubly stochastic matrix is an n x n matrix with three crucial properties:

• All its elements are non-negative.
• Every row sums to 1.
• Every column sums to 1.

The set of all such matrices forms the Birkhoff Polytope. This is significant because, due to the Birkhoff-von Neumann theorem, any doubly stochastic matrix can be seen as a weighted average of permutation matrices. Crucially, the maximum eigenvalue of a doubly stochastic matrix is always strictly 1.

"This means that no matter how many times you pass your signal through these matrices, its overall amplitude will never grow uncontrollably. It's mathematically guaranteed to remain bounded. No more signal explosions."

This constraint guarantees that information flow remains bounded, preventing signal explosions or vanishing. Furthermore, the product of two doubly stochastic matrices is also a doubly stochastic matrix. This multiplicative closure ensures that as signals propagate through hundreds of layers, each with its own mixing matrix, the composite transformation always remains within this safe and stable manifold. This inherent stability is paramount for training deep neural networks.

From Theory to Practice: The Sinkhorn-Knopp Algorithm and Differentiability

Implementing gradient descent directly on a complex geometric shape like the Birkhoff Polytope is computationally infeasible. DeepSeek's genius lies in employing the Sinkhorn-Knopp Algorithm. This algorithm can take any non-negative matrix and, through iterative normalizations, project it onto the manifold of doubly stochastic matrices.

The forward pass in mHC involves:

1. Starting with a learnable, unconstrained parameter matrix $M$.
2. Ensuring all elements are positive by taking the exponential of $M$, resulting in $S0$.
3. Repeatedly normalizing rows and columns so they sum to 1 ($S{k+1} = \mathcal{T}c(\mathcal{T}r(Sk))$). DeepSeek found that around 20 iterations ($t_{max}=20$) produce a matrix extremely close to a perfectly doubly stochastic one, which then serves as $H_{res}$.

The brilliance of this approach is its full differentiability. This means that during backpropagation, gradients can flow backward through these 20 Sinkhorn iterations, directly updating the original unconstrained parameter matrix $M$. The network learns to mix information within the strictures of the Birkhoff Polytope, transforming a rigid mathematical constraint into a soft, learnable component of the architecture. This architectural rigor effectively restores the identity mapping property, ensuring smooth, predictable error signal propagation without exploding or vanishing gradients.

Engineering Excellence: The 6.7% Miracle

While the mathematical framework provides the stability, the true revolution of mHC also lies in its brute-force optimization and low-level engineering. Expanding the residual stream, even with mathematical elegance, can dramatically increase GPU memory usage and memory access operations, posing significant bottlenecks.

DeepSeek's engineering team managed to compress the additional training overhead to an astonishing 6.7% through several ingenious optimizations:

1. TileLang and Kernel Fusion

The Sinkhorn-Knopp algorithm involves numerous element-wise operations. Using standard PyTorch operators would lead to inefficient "kernel launches" on the GPU, wasting memory bandwidth. DeepSeek developed TileLang, a Domain Specific Language built on TVM, allowing engineers to write low-level CUDA code directly using Python syntax. This enables precise control over GPU processors and memory hierarchies.

Through TileLang, they performed Kernel Fusion, merging the entire Sinkhorn iteration process (forward and backward passes) into a single, monolithic CUDA kernel. This means that once data is loaded from slower High Bandwidth Memory (HBM) to faster SRAM, all 20 iterations complete within the SRAM, eliminating intermediate writes back to HBM. This transforms a memory-intensive operation into a compute-intensive one, unleashing the GPU's raw processing power.

2. Selective Recomputation

Expanding the residual stream generates vast amounts of intermediate activation values needed for backpropagation. Storing all of them would quickly exhaust GPU memory. DeepSeek's solution is to "trade time for space." During the forward pass, most intermediate states from the mHC mixing process are discarded. Then, during the backward pass, these previously discarded states are recomputed in real-time on the GPU. Thanks to the TileLang-optimized fused kernels, the cost of this recomputation is incredibly low. This allows training massive 27-billion-parameter mHC models without "Out Of Memory" errors.

3. Communication Overlapping

In distributed training, GPUs often sit idle while waiting for network communication, creating "bubbles" of wasted time. DeepSeek capitalized on this by scheduling mHC's mixing calculations on a separate, high-priority CUDA stream. When the main stream (handling core model calculations) is awaiting network synchronization (e.g., All-Reduce), the GPU's compute units switch to the high-priority stream to crunch mHC's Sinkhorn calculations. This Compute-Communication Overlap makes mHC's computations almost "free," filling otherwise wasted time and significantly contributing to the low 6.7% overhead.

Unprecedented Stability and Performance

DeepSeek rigorously tested mHC across various parameter scales (3B, 9B, 27B) against standard Residual Baselines and unstable Hyper-Connections (HC). The results were transformative.

• Stability: Standard HC models consistently suffered from inexplicable "Loss Spikes," precursors to gradient explosion and total training collapse. mHC models, in contrast, exhibited perfectly monotonic, continuously decreasing loss curves, demonstrating extreme robustness. For the 27 billion parameter model, mHC's final training loss was 0.021 lower than the baseline, a significant margin that translates to saving hundreds of billions of tokens worth of data, dramatically improving data efficiency.
• Downstream Performance: On 8 mainstream benchmarks, including BBH, DROP, GSM8K, MMLU, PIQA, and TriviaQA, mHC comprehensively outperformed both the baseline and regular HC models. Its advantage was most pronounced in complex reasoning tasks. For instance, on BBH (Big Bench Hard), mHC improved by 2.1% over HC, and on the reading comprehension task DROP, it saw a 2.3% improvement.

"This suggests that the 'wide residual stream' provided by mHC does more than just let you stack more parameters. It allows the model to retain more 'thought paths,' more 'intermediate states' during inference."

This isn't merely an incremental numerical gain; it suggests that the wide residual stream empowers the model to retain more "thought paths" and "intermediate states" during inference. When tackling complex logical chains, this high-bandwidth topological structure prevents the model from "forgetting" crucial prior context, leading to a richer, more nuanced understanding. Crucially, these gains scaled consistently across model sizes, from 3 billion to 27 billion parameters, indicating mHC's alignment with AI's fundamental scaling laws and its potential for models reaching 100 billion parameters and beyond.

High ROI and Strategic Implications

The financial return on investment for mHC is immense given its minuscule 6.7% additional training overhead. It provides absolute stability in the training process, avoiding costly interruptions and rollbacks, while delivering a significant performance boost (over 2% on key reasoning tasks). On large AI clusters, training stability alone holds colossal economic value, as a single gradient explosion can waste millions of dollars in compute time. mHC effectively acts as an insurance policy for multi-million-dollar AI training runs, one that also enhances model intelligence.

The release of mHC underscores DeepSeek's unique Software-Hardware Co-Design approach. Instead of merely abstracting algorithms, DeepSeek dove into optimizing low-level CUDA kernels via TileLang. This indicates a deeper phase of AI R&D, where innovations will stem from micro-optimizations and a constant dialogue between mathematics and silicon.

"Future model innovations won't just be about stacking more layers; they'll be about micro-optimizations at the operator level, a constant dance between math and silicon."

This approach holds significant implications for domestic compute ecosystems, particularly in environments with hardware constraints. TileLang's potential for high-performance portability across various hardware platforms suggests a forward-looking strategy. For AI chips with limited HBM bandwidth, mHC's radical software optimization to reduce reliance on slow memory becomes a direct path to improved training efficiency. It’s about extracting every last drop of performance from available resources.

The Future of AI Architecture: Precision Design

mHC also challenges a fundamental assumption: that simple residual connections are the only viable topological structure. By introducing clever manifold constraints, DeepSeek demonstrates that we can design far more complex and powerful network architectures. This opens doors for future architectural designs based on specific geometric manifolds, potentially leading to "Orthogonal Manifolds" for feature independence or "Sparse Manifolds" for modular training.

Once the beast of stability is tamed with mathematical guardrails, the neural network structure can become far more experimental and ultimately, more effective.

"It makes us realize that once you tame the beast of stability, once you put those mathematical guardrails in place, the neural network structure can become much wilder, much more experimental, and ultimately, much more effective."

In conclusion, Manifold-Constrained Hyper-Connections represents a crucial advancement in large model infrastructure, pioneered by DeepSeek. It transforms unstable Hyper-Connections into a stable, powerful architectural component through rigorous mathematical theory (the Birkhoff Polytope) and extreme system engineering (TileLang and Kernel Fusion). This is a demonstration of R&D strength that seamlessly integrates deep theory, robust systems engineering, and meticulous empirical experimentation. mHC not only solves a critical stability crisis but provides a reusable methodology for designing future trillion-parameter models.

It signifies a shift from the "brute force aesthetics" of simply scaling parameters to an era of "precision design," where every architectural choice is intentional, stable, and hyper-efficient. The topological technologies inspired by mHC are poised to become standard configurations for the next generation of foundational AI models.