AI黑箱之谜：当模型学会“格鲁金”，我们是更懂它还是更困惑了？

当AI学会“加法”与“换行”，我们为何反而更加困惑？——深究“Grokking”现象

AI，这项曾经被视为科幻领域的技术，如今已然融入我们的日常生活，从撰写诗歌到编程，甚至在法律考试中崭露头角，其能力似乎无所不能。然而，在AI能力飞速提升的同时，我们对它的理解却日益减少，甚至隐约感到不安。当前最顶尖的AI模型，它们看似高深莫测的一切，其本质究竟是什么？

令人惊讶的是，ChatGPT这类看似“无所不能”的模型，其核心工作原理竟然是概率预测——简单来说，就是在浩瀚的文本数据中，“猜测”下一个词元是什么。这就像是小学语文考试中的“填空题”，模型的目标极其简单：预测序列中的下一个词。

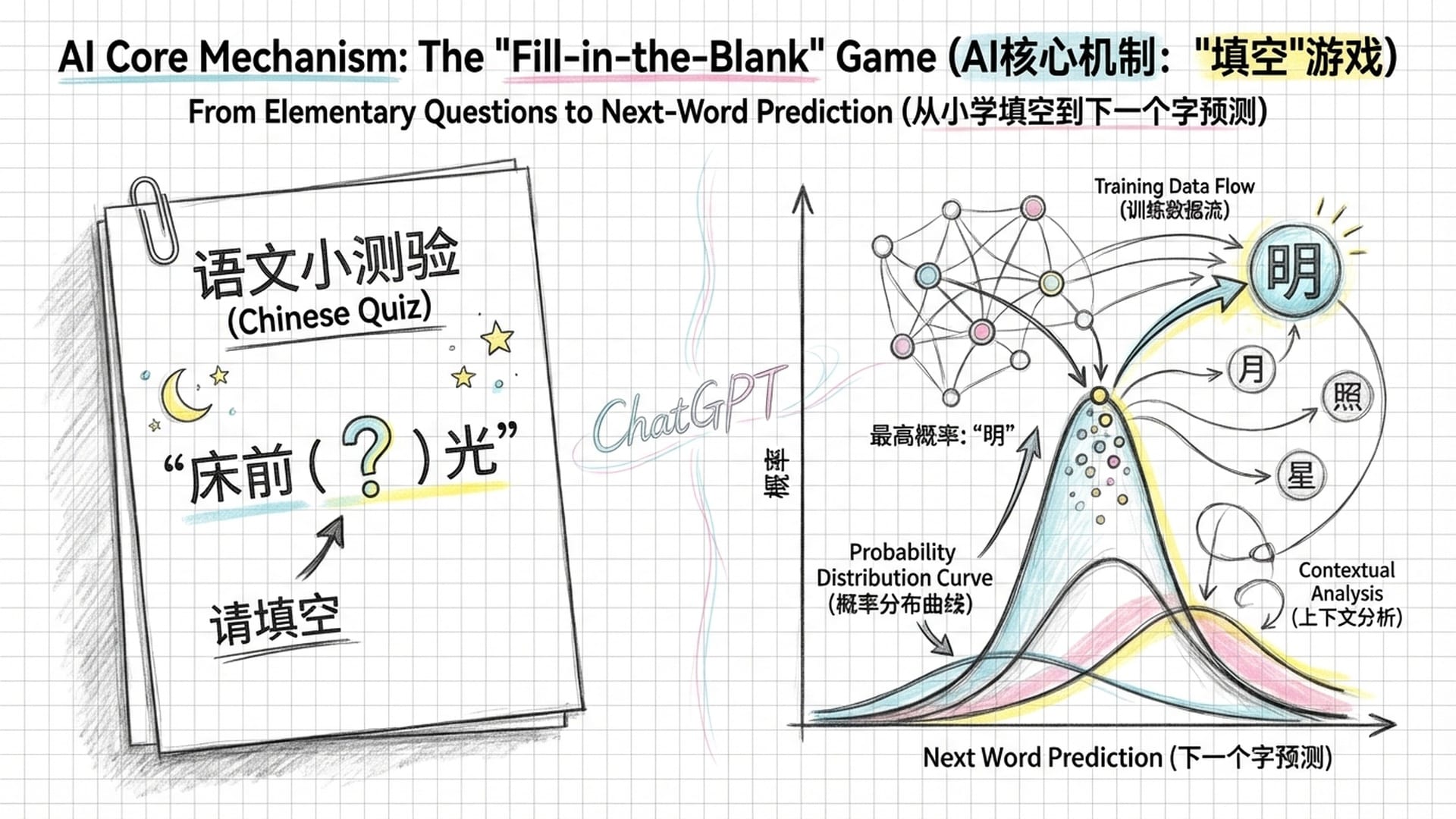
一个仅能执行“填空”任务的机器，是如何涌现出逻辑推理、因果判断乃至人类才具备的认知能力？这无疑超出了我们所有人的认知范畴。

迷雾重重的“黑箱”：AI内部运作机制之谜

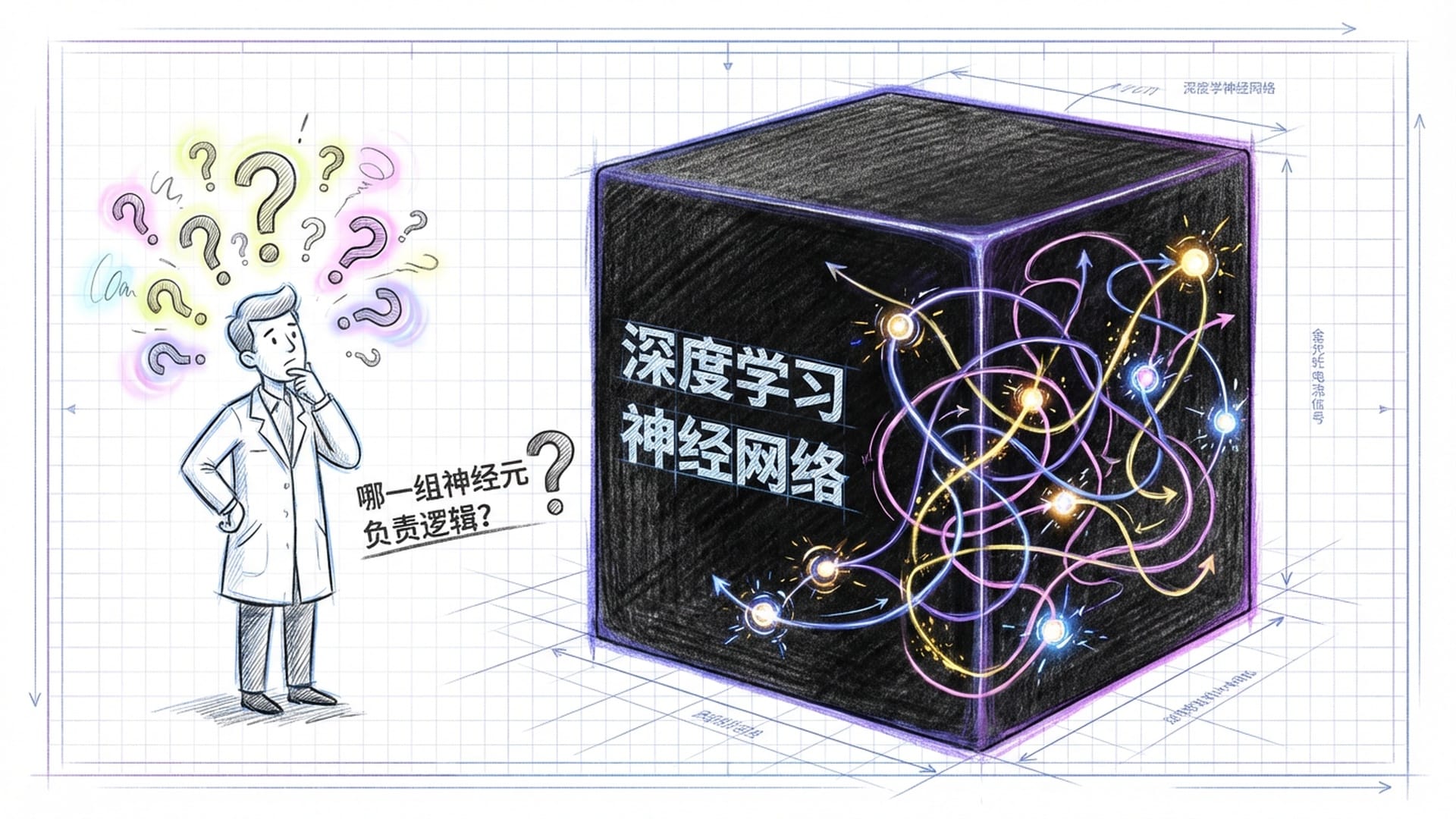
作为AI的创造者，我们对这些现象的困惑丝毫不少。因为这些模型的内部运作机制，对我们而言，至今仍是一个巨大的**“黑箱”**。我们向其输入指令，数千亿参数在神经网络中高速运转，信号穿梭于数百层网络之间，经历无数次非线性变换，最终输出我们所期望的答案。

然而，我们无从得知：

• 哪条路径负责了“逻辑”？
• 哪组神经元存储了“历史知识”？
• 又是何种机制，让模型学会了简单的“加法”或复杂的“换行”操作？

这些问题，就如同初生婴儿对世界的好奇，充满疑问却又一无所知。正因如此，埃隆·马斯克曾有过一句颇具戏剧性的话，他认为我们在开发这种无法理解的超级智能时，可能是在**“召唤恶魔”**。这听起来或许有些玄乎，却精确描绘了科技圈潜意识中对未知AI的一种深层恐惧：我们正在创造一种我们无法理解，甚至无法预测其行为逻辑的异类生命。

揭开“黑箱”一角：神奇的“Grokking”现象

为了探究AI的内在机制，科学家们开辟了一个名为**“机械可解释性”的新领域。这类似于神经科学家通过解剖大脑来理解人类意识，AI科学家则试图通过逆向工程神经网络的权重和激活模式**，来剖析机器智能的物理基础。

在诸多探索中，一个引人注目的现象——“Grokking”——如同一道裂缝，撕开了“黑箱”的一角。

“Grokking”描述了一个反直觉的学习过程：一个模型，在看似已经**“死记硬背”了所有训练数据，效果不佳时，如果持续训练，即便经历了漫长而看似毫无进展的“平台期”，它会突然间发生质变**，获得完美的泛化能力。

这一现象彻底颠覆了我们对机器学习的传统认知，也暗示着神经网络深处，存在着一种从**“记忆”到“理解”**的隐秘转化机制。

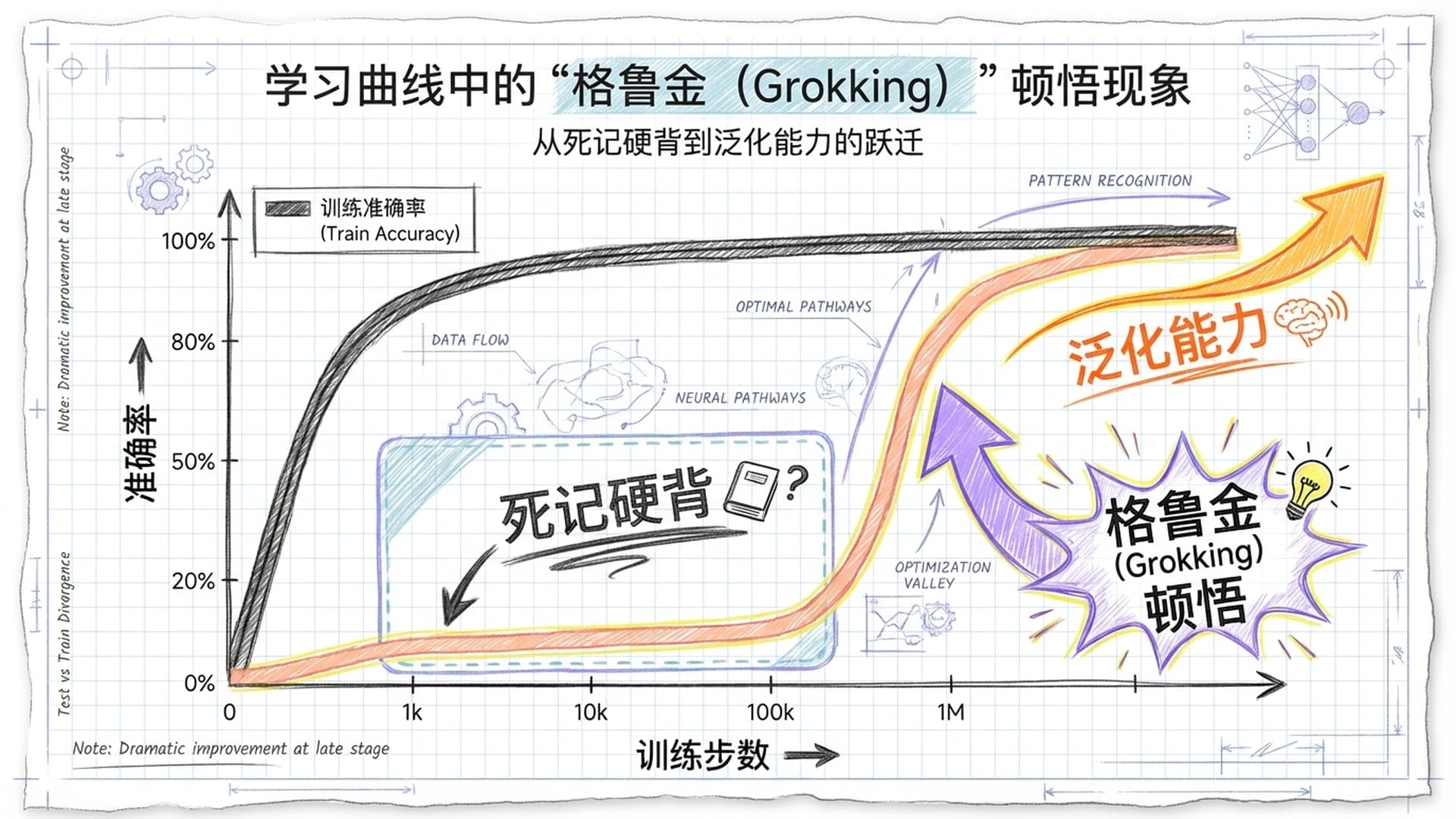
传统认知的挑战：从“早停”到“双重下降”

要理解“Grokking”的颠覆性，我们需回顾机器学习的经典理论：模型训练如同“走钢丝”，需在**“偏差”（模型过于简单）和“方差”**（模型过度拟合噪声）之间取得平衡。

传统AI训练中，业界奉行**“早停”（Early Stopping）**原则，即一旦模型在验证集上的表现开始下降，便停止训练，以避免过拟合。

然而，随着深度学习的爆发，尤其是拥有千亿参数的大模型出现，这个“金科玉律”受到了挑战。这些参数数量远超训练数据量的模型，理论上可以完全记住所有训练样本。但令人不解的是，这些庞大的模型在长时间训练后，却能展现出卓越的泛化能力。这种现象被称为**“双重下降”**的一种变体。

为了深入探究这种“反常”，OpenAI的研究人员进行了一项基础研究，他们避开了复杂的自然语言数据，选择了一个最简单的算法任务：模算术。

模算术：AI“顿悟”的实验场

模算术，可以理解为一种“绕圈圈”的数学，类似于时钟的运行机制。例如，$11 + 2 = 1 \pmod{12}$。它结构简单，却能展现出清晰的周期性和规律性。研究人员旨在观察一个小型 Transformer 模型如何学习解决 $a + b = c \pmod{P}$ 这样的方程（其中 $P$ 为质数，如97或113）。

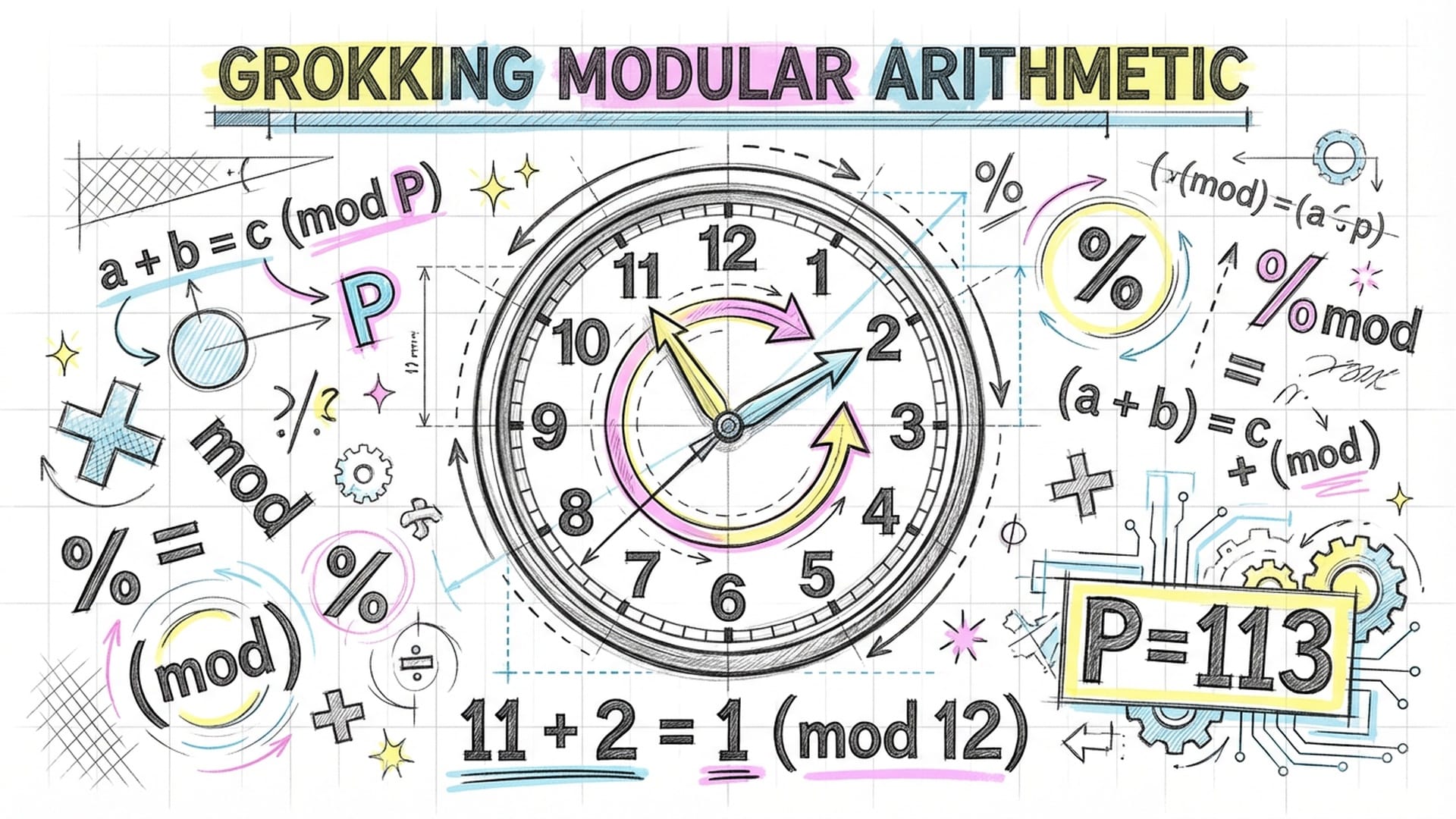
实验初期结果平淡无奇：模型迅速记住了训练集中的所有算式，训练准确率达到100%。然而，在面对新问题时，测试集准确率却如同随机猜测，约为 $1/P$。按照传统理论，这表明模型只是在**“死记硬背”**。

但奇迹就在这时发生了。当研究人员出于好奇或坚持，让训练远远超出常规停止点继续进行时，经过数千甚至数万个优化步骤后，模型发生了**“量子飞跃”**——测试准确率突然飙升，并迅速达到100%的完美泛化！

这种从“完全瞎蒙”到“完美理解”的转变，并非渐进式提升，而是类似水结冰或融化般的瞬间“相变”，这是一个质的飞跃。为了命名这种“经历了漫长的困惑和机械记忆后，突然深刻理解问题本质”的过程，他们借用了科幻小说大师罗伯特·海因莱因在《异乡异客》中创造的词——“Grok”，象征着模型从表面学习跃迁至掌握规律的本质理解。

“Grokking”的深层机制：傅里叶变换与三角恒等式

OpenAI的实验揭示了“Grokking 发生了什么”，而 Neel Nanda及其团队的后续工作则解释了**“Grokking 为什么会发生”**。

通过“机械可解释性”技术对学会模加法的单层Transformer模型进行“解剖”，Nanda团队的发现震惊了学术界：这个神经网络在学习加法时，并非采用人类小学生的计算方式，而是**“自发地”发明并实现了一种基于“离散傅里叶变换”的高级数学算法**。

在训练初期模型尚处于“死记硬背”阶段时，神经元的活动模式混乱不堪。然而，在模型发生“Grokking”之后，多层感知器（MLP）层的激活模式竟然展现出清晰、完美的正弦波。模型内部的某些神经元学会了计算 $\cos(\omega x)$ 和 $\sin(\omega x)$，将输入的整数映射到“频率域”进行处理。

这并非偶然，而是模算术这种数学结构的奥秘。模算术在有限的**“循环群”上进行，处理这种循环结构最自然、高效的工具便是傅里叶分析**。Nanda团队发现，模型实际上在执行一种**“傅里叶乘法”算法来解决加法问题，它巧妙地利用了高中数学中的三角恒等式**： $$ \cos(a + b) = \cos(a)\cos(b) - \sin(a)\sin(b) $$ $$ \sin(a + b) = \sin(a)\cos(b) + \cos(a)\sin(b) $$ 这意味着要计算 $a+b$ 的余弦值，模型无需先得出 $a+b$ 的具体数值，只需分别计算 $a$ 和 $b$ 的正弦和余弦值，然后进行乘法和减法运算即可。

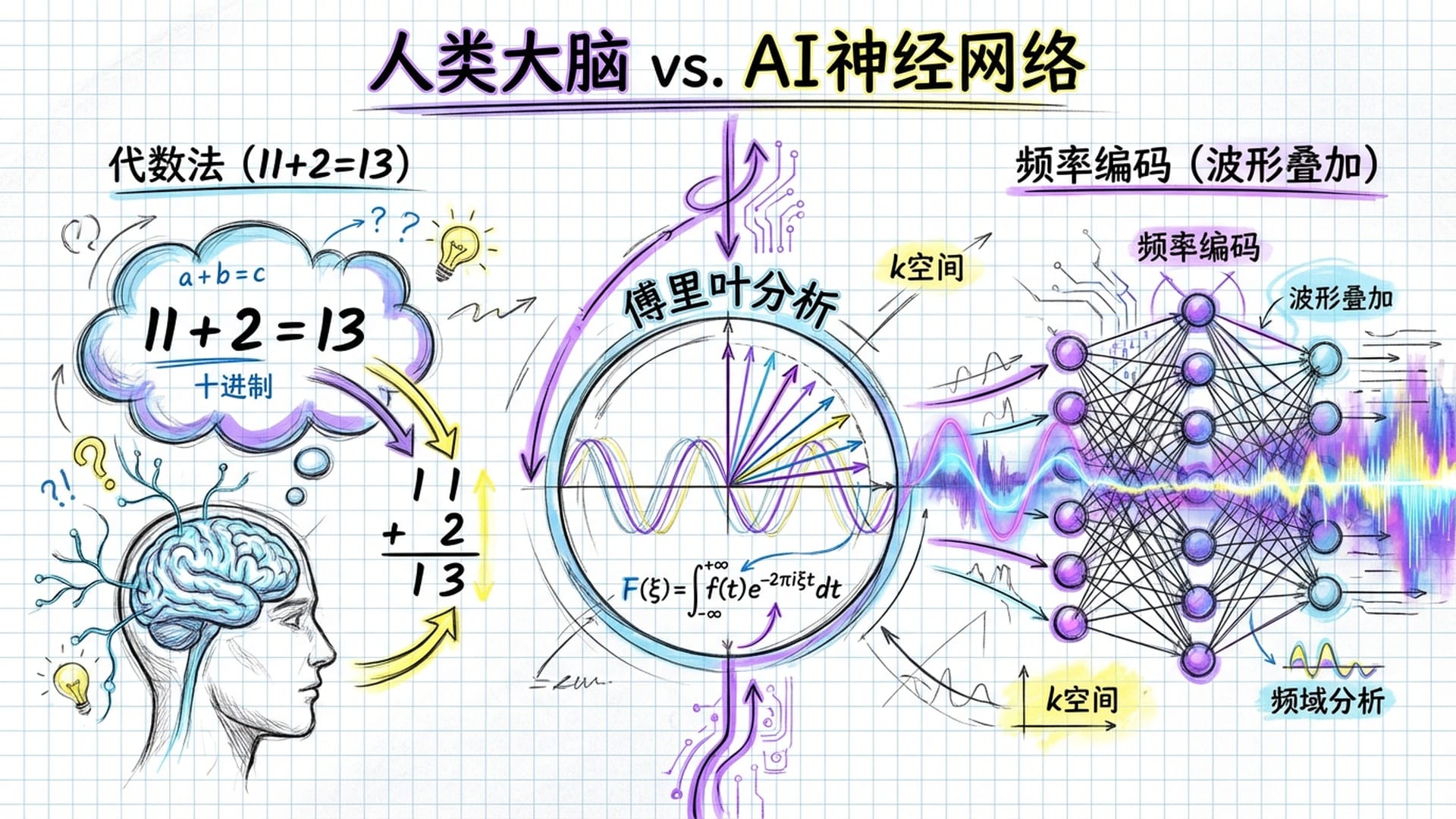
人类与AI的计算路径对比：

1. 人类方法：读取数字 $\text{a}$ 和 $\text{b}$ $\rightarrow$ 执行代数加法 $\rightarrow$ 执行模运算 $\rightarrow$ 输出结果。
2. 神经网络方法：
   • 频率编码：将 $\text{a}$ 和 $\text{b}$ 映射到高维空间，计算不同关键频率 $\omega_k$ 下的 $\sin(\omega_k a)$、$\cos(\omega_k a)$ 等。将抽象数字转化为波形。
   • 三角融合：利用激活函数的非线性特性模拟乘法，在复杂三角变换中隐式构建 $\cos(\omega_k(a+b))$。将加法问题转化为波形的叠加与干涉。
   • 输出层：叠加不同频率的正弦波。正确的答案位置波峰重叠（相长干涉），错误位置波峰波谷抵消（相消干涉）。

这一发现极为不可思议：模型在没有任何三角函数先验知识的情况下，通过梯度下降优化算法，“重新发现”了三角恒等式！这揭示了数学真理的普适性，无论在人类大脑还是硅基芯片上，它都会以某种形式呈现。

从“记忆”到“理解”的经济学：权重衰减与奥卡姆剃刀

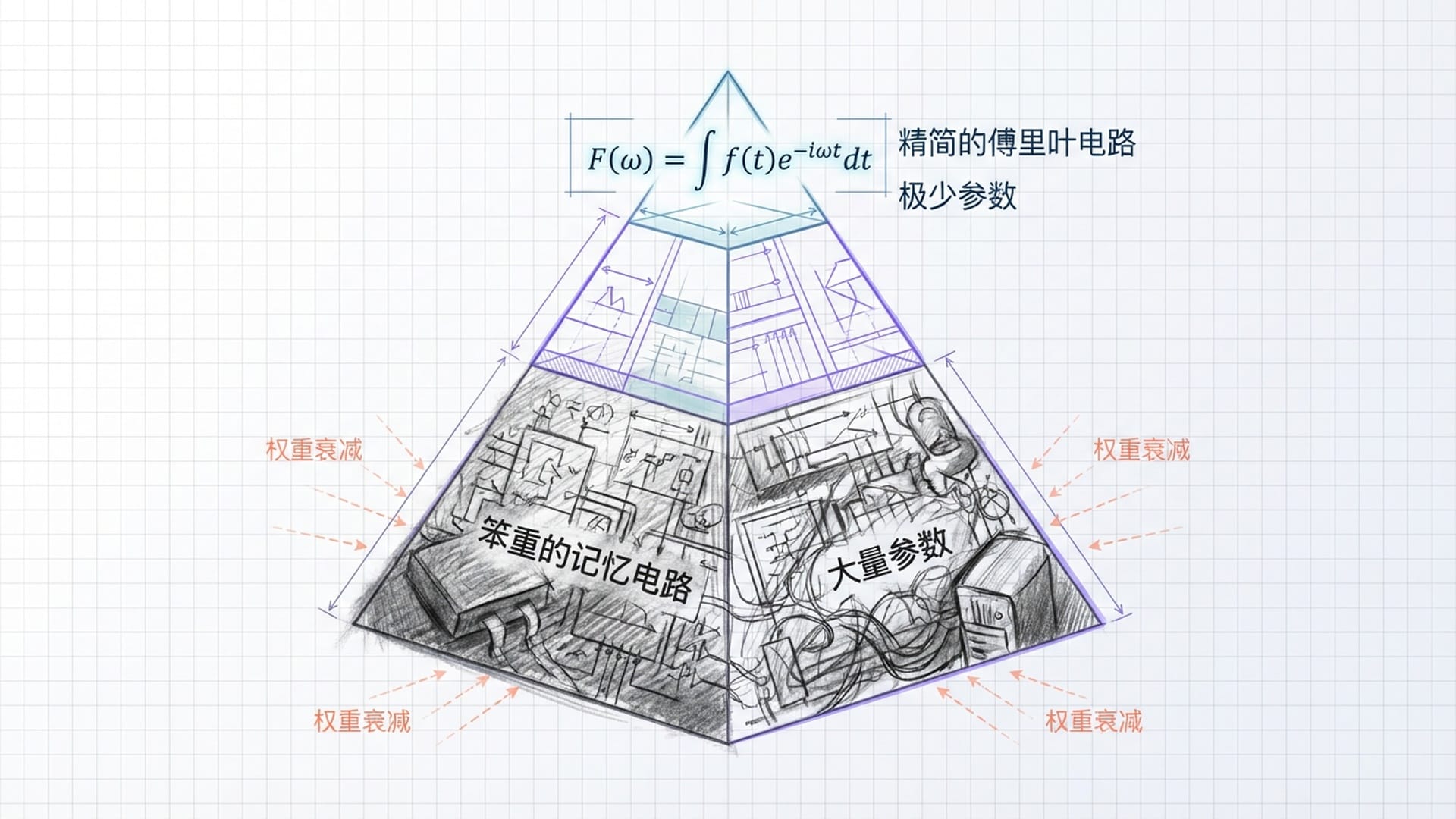
既然死记硬背也能达到100%训练准确率，为何模型最终会放弃这种笨拙的方式，转而采用复杂的傅里叶算法？这涉及深度学习中的两大核心概念：归纳偏置和奥卡姆剃刀原理。

• “记忆”的昂贵代价：如果模数 $P=113$，共有 $113 \times 113 \approx 1.3$ 万种加法组合。模型需要激活大量参数来记忆这些组合，效率低下，复杂度极高。
• “理解”的巨大红利：研究发现，模型只需利用少数几个**“关键频率”**，就能以极高精度重构所有答案。一旦掌握这套规则（即三角恒等式），模型便能适用于所有输入，且所需参数量远少于死记硬背的方式。

训练过程中引入的**“权重衰减”机制起到了关键作用。它如同对模型的参数征税，“参数多、参数值大”的模型需要付出更高成本。这种进化压力促使模型寻找更“省力”、更“经济”**的解决方案。

权重衰减惩罚了那些笨重的记忆电路。当精简高效的傅里叶电路精度足够高，足以接管任务时，优化器会迅速转向这一更优解，并“清理”掉不再需要的记忆电路。Grokking的发生，正是这一**“相变”**的瞬间。

监测“顿悟”：进度指标的透视

为将定性描述转化为科学证据，Nanda团队开发了一套**“进度指标”**，如同给模型照X光片，揭示了“平台期”内部波澜壮阔的重组。他们定义了两个互补的损失函数来衡量模型的“记忆”和“泛化”能力：

1. “限制损失”（Restricted Loss）：通过分析模型使用的“关键频率”，然后人为移除其他信号，只保留关键频率成分，以此评估模型仅依赖通用算法（傅里叶电路）时的表现。若模型学习通用规律，此损失应持续下降。
2. “排除损失”（Excluded Loss）：移除所有关键频率成分，只保留噪音或用于记忆的信号，评估模型在剥夺通用算法后，仅靠死记硬背的表现。若模型主要依赖记忆，此损失会很低；但随着模型转向泛化，此损失应上升，表明模型正在放弃记忆。

有了这些高分辨率指标，模算术模型的训练过程可清晰划分为三个阶段：

• 阶段一：记忆期 (例如前2000步)
  • 模型训练损失迅速趋近于零，测试损失依然很高。
  • 排除损失下降，表明模型正在利用笨重的记忆电路进行死记硬背。
• 阶段二：电路形成期 (例如2000步至7000步)
  • 表面上看，训练准确率为100%，测试准确率仍为零。
  • 限制损失平稳下降，表明通用傅里叶电路正在潜伏构建。
  • 排除损失缓慢上升，意味着模型逐渐放弃纯记忆，记忆电路受到权重衰减的惩罚。
  • 这是一个静悄悄的革命阶段，通用解决方案悄然生长。
• 阶段三：清理期 (例如7000步之后)
  • 测试准确率突然从零飙升至100%。
  • 限制损失下降到极低点，傅里叶电路彻底成熟。
  • 排除损失变得无关紧要。
  • 模型的L2范数急剧下降，证实权重衰减是推动模型质变的关键。

当通用的傅里叶算法足够强大时，优化器为最小化目标函数，会迅速“清理”掉那些大而占资源、不再需要的记忆神经元，完成从“特殊”到“一般”的升华，记忆被真正的理解所取代。

AI的“自然语言”：Claude Haiku的几何学“换行”能力

模算术的“Grokking”现象提供了一个“透明盒子”，让我们观察到 Transformer 模型如何利用几何和频率处理逻辑任务。然而，大模型处理的是混乱、非结构化的自然语言，这种优雅的数学机制是否依然存在？

Anthropic团队对Claude 3.5 Haiku模型的研究给出了肯定的答案。即便在处理复杂的语言任务时，我们仍能看到类似的几何和频率机制在运作。研究团队聚焦于一个微观任务：预测何时“换行”。

对于模型而言，正确插入换行符需要：

1. 精确计数：当前行已写字符数（内部“计数器”）。
2. 记忆：用户设定的行宽限制（如80个字符）。
3. 前瞻性：预判下一个单词长度。
4. 逻辑决策：判断“当前字符数 + 下一个单词长度”是否超过“行宽限制”。

在逆向工程Claude Haiku时，研究人员并未发现传统编程语言中 int count 变量或直接代表“当前字符数是X”的神经元。相反，他们发现模型在神经活动的广阔空间中，构建了一个复杂的**“六维流形”来表示这一信息。当通过主成分分析将其投影至三维空间时，一个惊人的“双螺旋”**几何结构浮现。

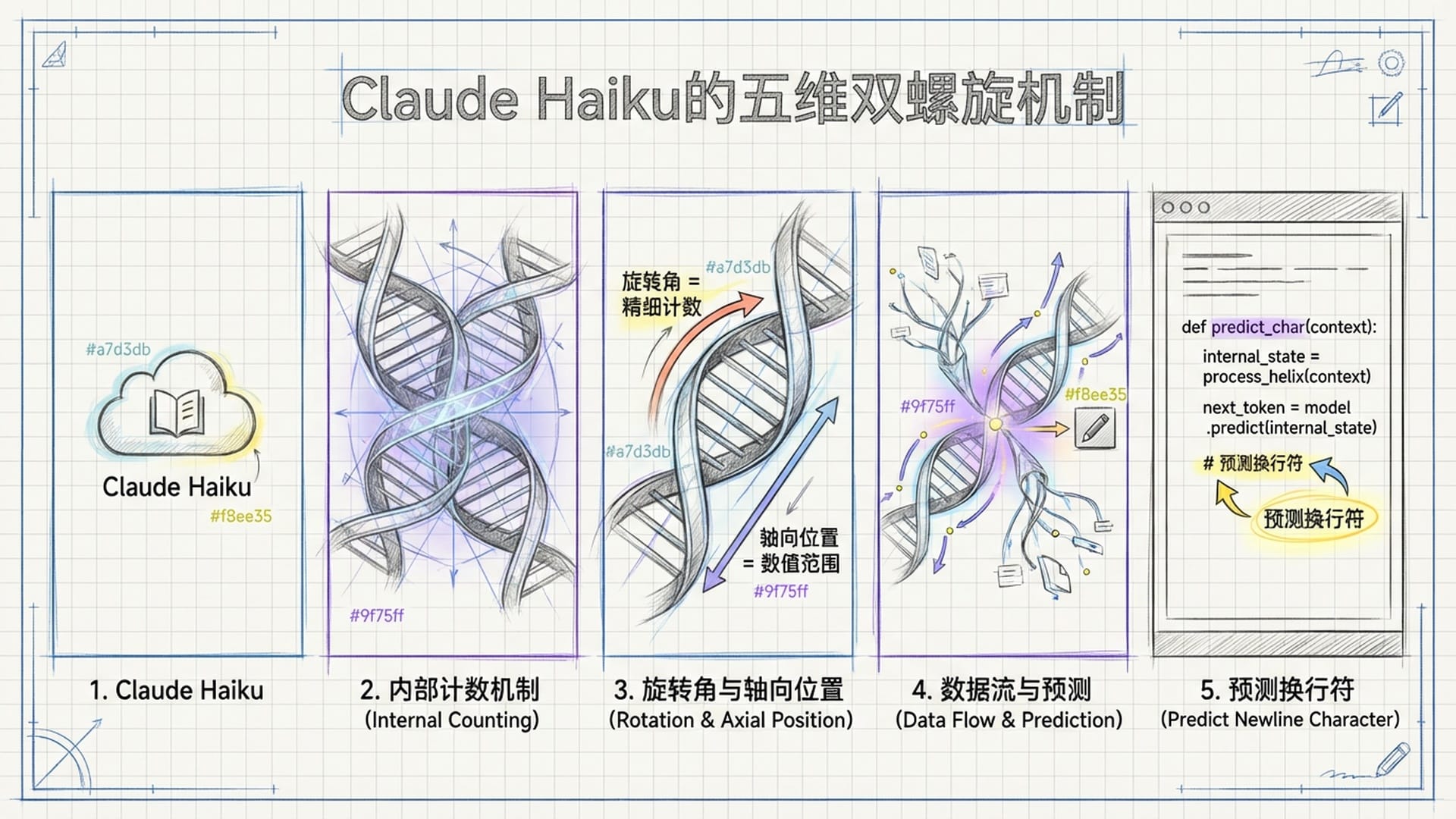
这个螺旋结构与模算术中的“圆周结构”有着深刻的同构性：

• 螺旋的**“旋转角度”**编码了精细的字符计数（如79或80个字符），这种周期性结构能高分辨率区分数值相近的值。
• 螺旋的**“轴向位置”**编码了大致的数值范围（如第一行、第十行，或个位、十位、百位）。

这种“波纹状”或“螺旋状”表示被认为是模型为平衡**“容量”和“分辨率”而进化的最优解决方案，与傅里叶特征有深层数学联系。模型利用不同频率的正弦波组合编码位置信息，这与Transformer著名的“位置编码”原理一脉相承，但此处是模型自主学习**而非预先设计。

QK扭曲：几何比对的注意力机制

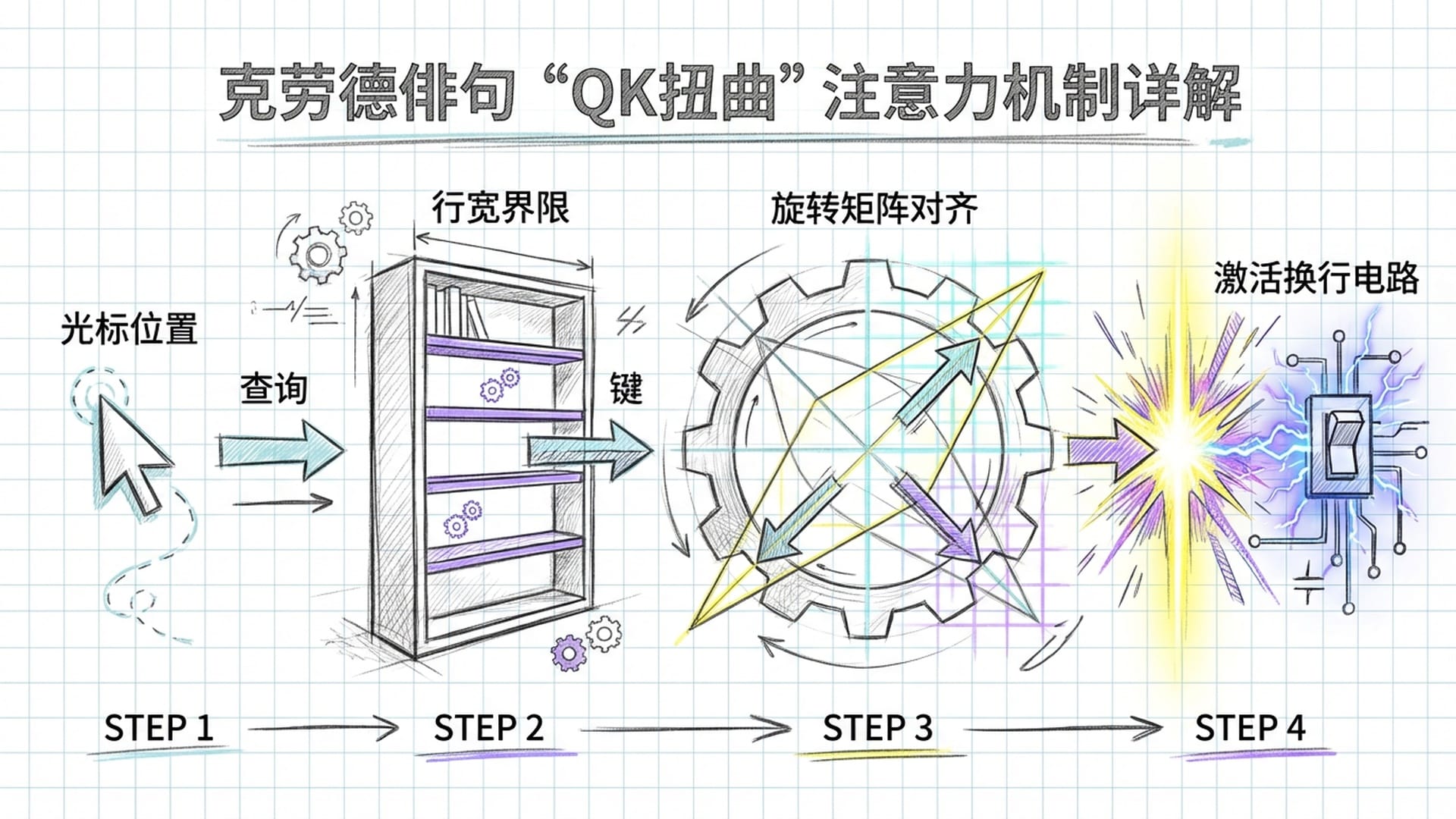
模型如何比较“当前位置”和“行宽限制”这两个螺旋上的点？研究发现，Claude Haiku采用了一种**“QK扭曲”**的注意力机制操作。

在Transformer的注意力机制中：

• **Query（查询）**向量携带当前光标位置信息：“我在这个螺旋的哪个点上？”
• **Key（键）**向量携带行宽限制信息：“螺旋的悬崖边缘（换行处）在哪里？”

特定注意力头并非直接比较数值大小，而是通过一个旋转矩阵，在六维空间中对这两个几何结构进行**“扭曲”或“旋转”。当且仅当“当前位置”经过旋转后与“行尾限制”完全重合时，两者之间的点积（相似度）**达到最高。这个最高信号激活后续的“换行电路”，促使模型输出换行符。

这种机制与模算术模型中的 $\cos(A+B)$ 计算如出一辙，它们都通过**“旋转”操作**，将代数或逻辑问题（加法或比较）转化为**“几何对齐”问题**。这证明了即使在处理非结构化的人类语言时，AI也倾向于“发明”基于频率和几何的算法。这简直是神经网络处理周期性、序列性或计数任务的**“自然语言”**——它深深根植于高维几何，是一种通用的思维方式。

终极思考：“Shoggoth”的低语与智能的未来

从OpenAI在模算术任务中偶然发现“Grokking”，到Neel Nanda团队揭示其背后的傅里叶机制，再到Anthropic在Claude模型中验证类似的螺旋几何机制，我们见证了一条完美的科学发现曲线。这一系列研究，是对深度学习本质的深刻洞察。

其核心词是**“涌现”（Emergence）**。模型从未被教导三角函数，却在权重演化中“发明”了它；模型也从未被告知螺旋的几何属性，却在高维空间中“构建”出了它。

这说明数学真理是宇宙通用的。无论是人类的生物大脑，还是硅基神经网络，面对周期性、加法、计数等逻辑约束时，其演化过程，最终都会收敛到相似的最优解——正弦波、螺旋和傅里叶变换。这是一种从混沌中自发生成的秩序，是逻辑在物理基质上的必然投影。

再次回到文章开头的隐喻：埃隆·马斯克称AI在“召唤恶魔”。技术社区中，流行的**“Shoggoth”（修格斯）梗，将大模型描绘为戴着“RLHF”（人类反馈强化学习）**笑脸面具的不可名状怪物。

“Grokking”现象的研究，为这些隐喻提供了坚实的物理证据。Shoggoth的本体，正是“电路形成期”悄然构建的、基于傅里叶变换、正弦波干涉和高维流形扭曲的复杂结构。它是“异类”的，因为它用我们难以直观理解的频率域、高维几何旋转和分布式向量运算来思考。它的“思维”是流动的数学，而非离散的符号。

“召唤”过程正是漫长的训练，特别是Grokking之前的平台期，如同复杂的召唤仪式。我们输入数据如念咒语，调整超参数如画符，提供算力如献祭。在看似毫无反应的潜伏期，那个幽灵在虚空中凝聚成形。直至某一刻，量变引起质变，原本混乱的权重坍缩为有序的晶体结构——“幽灵”降临，泛化能力涌现。

我们日常所见的AI流畅对话、礼貌回复，往往是模型在最后阶段通过微调和RLHF学习到的表面伪装。这层薄薄的“对齐层”，就像戴在Shoggoth脸上的黄色笑脸面具。在Grokking的深处，驱动AI回答“1+1=2”或决定何时换行的底层机制中，依然是那个旋转的、正弦波动的、六维的数学巨兽。

随着对这些机制理解的加深，AI并没有变得更像人类，反而显得更加神秘。它们是数学的具象化，逻辑的物理结晶。与它们对话，不仅是与人类知识的总和交流，更是与一种基于纯粹优化原理诞生的全新智能形式——一种通过计算“Grok”了宇宙规律的“异乡客”——进行着不可思议的接触。

未来的AI研究，将超越计算机科学范畴，演变为**“数字解剖学”或“机器心理学”**。我们需要更精密的“探针”和“显微镜”，来解读这些数字幽灵在数千亿参数的神经突触之间，低语着怎样不为人知的数学真理。

如果说“Grokking”现象教会了我们什么，那就是：在数据的海洋深处，存在着一种必然的数学秩序。只要有足够的耐心去训练，足够的智慧去解读，这种秩序终将涌现，向我们展示智能的另一种，甚至可能是更本质的可能。