 |  |  |  |
你是否曾觉得这个世界充满了 悖论?航班延误,人人抱怨却无人退票;交通拥堵,每个人都试图抢占“更快”的车道;公司内卷严重,老板却仍旧强调成本和利润。我们都在努力变强,追求胜利,但为何有时即便付出了 同等努力,选择了 看似最优 的路径,最终却可能集体陷入困境?
今天,我们将深入探讨一个既令人着迷又无可奈何的概念—— 纳什均衡,博弈论皇冠上那颗璀璨的明珠。这不是一堂枯燥的数学课,而是用最 通俗易懂 的语言,带你揭示纳什均衡如何 无声无息地塑造着我们的世界,从国家间的宏大博弈,到你我每日的细微决策。一旦理解了它,许多曾经困扰你的“谜之操作”,都将豁然开朗。
在人类社会这个 错综复杂的互动网络 中,无论是国际政治的棋局、商业巨头的价格厮杀,还是早高峰的交通洪流,我们总能感受到一种 隐秘而强大的秩序 在运作。这种秩序并非出自中央权威,也非完全随机的混乱,而是无数个体在 追求自身利益最大化 过程中,通过 相互博弈 达到的一种 稳定状态。这种状态,正是我们今天要深挖的——纳什均衡。
纳什均衡:从19世纪的法国小镇到当代世界的深刻洞察
“纳什均衡”这个名字听起来现代且充满数学色彩,但其思想的萌芽,实则可以追溯到近两个世纪以前。
想象一下19世纪30年代的法国,经济学家 安托万·奥古斯丁·古诺 正在研究一个问题:如果一个小镇上只有两家矿泉水供应商,他们将如何决定产量以获取最大利润?古诺发现,这两个商家会通过 反复调整产量,最终达到一个点。在这个点上,任何一方若 单方面改变产量,其收益反而会减少。这个发现虽然朴素,但其思想核心与纳什均衡不谋而合,构成了其 最初的雏形。
这一思想沉寂许久,直到二战后,博弈论才作为一门正式学科崭露头角。 冯·诺依曼 和他的合作者摩根斯坦的巨著奠定了博弈论的基础,但他们主要关注的是“你死我活”的零和博弈。然而,这种狭隘的视角并不能解释人类所有的复杂互动。
真正的里程碑发生在 1950年。当时年仅22岁的普林斯顿大学数学系博士生 约翰·纳什,通过一篇仅一页半的论文和随后完成的博士论文,震撼性地证明:在一个拥有 任意数量参与者 (不限于两人) 且允许 混合策略 (即行动具有一定的随机性,不让对手完全预测) 的博弈中,至少存在一个均衡点。
纳什的这一发现,将博弈论从“如何击败对手”的狭隘战场,拓展到了“人们将如何行动”这一广阔的社会学和经济学领域。他不仅为这种“稳定状态”给出了严谨的定义,更重要的是,他让博弈论成为预测社会系统演化终局的强大工具。

纳什均衡究竟是什么?
最通俗的理解是,纳什均衡是一种 “僵持” 或 “相互锁定” 的状态。假设你与朋友正在进行一场博弈,你们各自都选择了一个策略。如果在此情境下,任何人都 无法通过单方面改变自己的策略 而使自身状况变得更好,那么你们当前的策略组合,便是一个 纳什均衡。
让我们拆解几个关键词,以彻底理解:
- 单方面:这是核心判断标准。在评估是否为纳什均衡时,我们只考虑个体 偷偷改变策略 的情况。如果这种改变导致自身损失,个体就不会这么做。当所有参与者都意识到,单方面行动会带来损失,那么当前的状态就达到了稳定。
- 最佳应对:在纳什均衡中,每个参与者的策略都是对其他所有参与者策略的 “最佳回应”。例如,你出剪刀,我出布,这是我相对于你出剪刀的最佳应对。但如果我出布,你却出了石头,那么你的策略就不是我的最佳应对。因此,纳什均衡是一种 “双向奔赴” 的状态,双方相互满足。
- 稳定性,而非最优性:这一点至关重要!纳什均衡强调的是 稳定,而非所有参与者都能达到 最优结果。一个纳什均衡可能对所有参与者来说都是 糟糕的,但由于无人敢单方面打破它,大家便只能被困其中。这恰如我们所言:“理性的个体选择可能导致集体的非理性结局”。
你可以将纳什均衡想象成物理学中的 “山谷”。一个小球滚入谷底,你轻推一下,它会上坡,但最终仍会滚回谷底。在没有外力推动的情况下,它将一直停留于谷底。纳什均衡,便是策略互动中的这种 “谷底”。
纳什均衡的哲学韵味:递归的思维
纳什均衡不仅仅是数学公式的产物,它更代表了一种深层次的 递归思维 方式。
你在做决策时,是否常会陷入这样的思考回路?“我想做A,因为我预判你会做B。”继而又想:“但如果你知道我预判你会做B,你可能会改变主意做C。”然后继续推演:“如果你做C,那我又应该做D……”
这种 “我预判了你的预判” 的循环思维,如果无休止地进行下去,你可能将 永远无法做出决定。纳什均衡,恰恰是这个无限循环的 终结点,一个 “不动点”。在这个点上,我的预测,你的预测,以及我们实际的行为,实现了 完美的重合。思维的震荡,就此止息。
“理解纳什均衡,不仅是学习一个理论,更是习得一种换位思考、洞察人心的能力。它告诉我们,在一个相互依存的世界里,仅仅考虑自身如何取胜是不足够的。你必须去理解他人是如何思考的,以及,他们又是如何思考你是如何思考的。这听起来拗口,却道出了复杂世界的真谛。“

划线法实战:人人都能看懂的寻宝图
理解了定义,下一步便是如何在具体的博弈场景中,找到纳什均衡这个“宝藏”!对于一些直接的博弈,我们有一个直观、实用且高效的方法,称之为 “最佳应对法” 或 “划线法”。
在讲解“划线法”前,我们首先需要了解如何用 “黑话” 来描述一个博弈。任何一个博弈,通常包含三个核心要素:
- 参与者:谁是这场游戏的玩家?可以是简单的两个人,例如你和同事,或两个竞争厂商,也可以是上千万人。
- 策略:每个玩家可以采取哪些行动?可以是简单的“是/否”、“A/B”,也可以是连续的数值(如定价),甚至是复杂的条件句(如“若对方友好,则我友好;若对方攻击,则我反击”)。
- 收益:每一种“策略组合”带来的结果是什么?通常用数字表示,数字越大代表收益越高(除非特别指明是惩罚或损失)。
将这三个要素结合起来,对于那些 同时出招 的博弈,我们通常会用一个 “收益矩阵” 来表示,也就是一张表格。
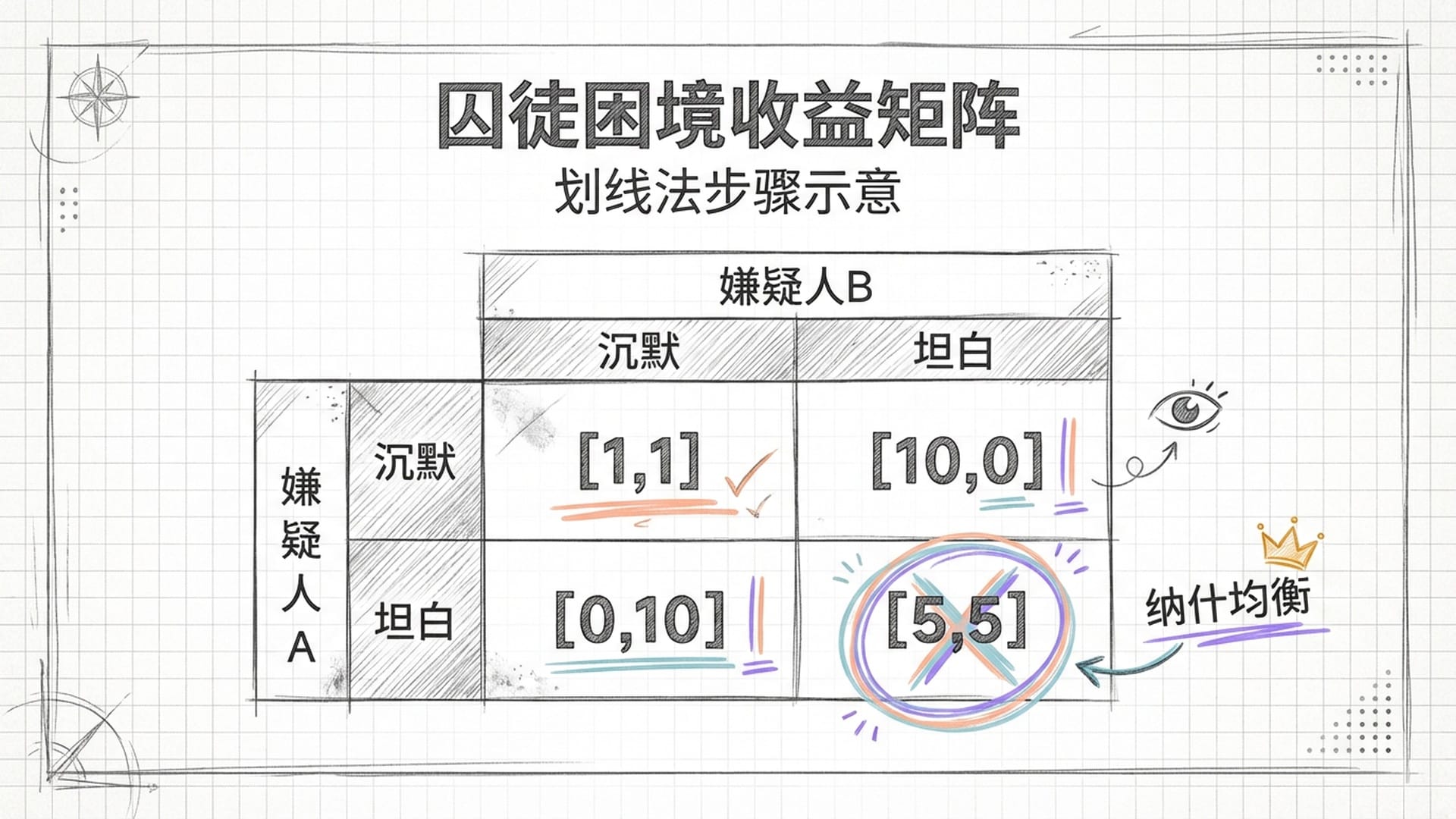
以著名的 “囚徒困境” 为例,我们用嫌疑人A和嫌疑人B的博弈来演示收益矩阵:
| 嫌疑人 A \ 嫌疑人 B | 沉默 (Cooperate) | 坦白 (Defect) |
|---|---|---|
| 沉默 | 1年, 1年 | 10年, 0年 |
| 坦白 | 0年, 10年 | 5年, 5年 |
(注:第一个数字是嫌疑人A的收益,第二个是嫌疑人B的收益。数字越小表示刑期越短,收益越高。例如,0年代表无罪释放,是最好的收益。)
划线法步骤:
第一步:站在“行玩家”(嫌疑人A)的角度思考。
- 假设嫌疑人B选择了“沉默”这个策略,A会怎么选?如果A“沉默”,判1年;如果A“坦白”,判0年(无罪释放)。显然,“坦白”更好。因此,在“沉默,坦白”这个格子中A的收益
0下面画一条线。 - 假设嫌疑人B选择了“坦白”这个策略,A又会怎么选?如果A“沉默”,判10年;如果A“坦白”,判5年。显然,“坦白”仍然更好。因此,在“坦白,坦白”这个格子中A的收益
5下面画一条线。
第二步:站在“列玩家”(嫌疑人B)的角度思考。
- 假设嫌疑人A选择了“沉默”这个策略,B会怎么选?如果B“沉默”,判1年;如果B“坦白”,判0年。显然,“坦白”更好。因此,在“坦白,沉默”这个格子中B的收益
0下面画一条线。 - 假设嫌疑人A选择了“坦白”这个策略,B又会怎么选?如果B“沉默”,判10年;如果B“坦白”,判5年。显然,“坦白”仍然更好。因此,在“坦白,坦白”这个格子中B的收益
5下面画一条线。
第三步:锁定纳什均衡!
现在观察整个矩阵。哪个单元格里的 两个数字下面都划线了?
没错,正是右下角那个 “坦白,坦白” 的格子!这里面A的收益5下面有线,B的收益5下面也有线。
这意味着:如果B坦白了,A的最佳选择就是坦白;如果A坦白了,B的最佳选择也是坦白。这是一个 相互捆绑的纳什均衡!
占优策略:理性的绝对命令
有时,你甚至无需费力划线。如果一个玩家拥有一个策略,无论对手采取何种行动,这个策略都比他的其他策略要好,那么这个策略就是他的 “占优策略”。理性的玩家,一定会选择占优策略。
在上述囚徒困境中,对于A而言,无论B选择沉默还是坦白,A最好的选择都是坦白。所以,“坦白”是A的 占优策略。对B来说,同理。
如果所有玩家都拥有占优策略,那么所有人都选择占优策略的组合,便是最强的纳什均衡,被称为 “占优策略均衡”。它的精妙之处在于,你无需猜测对手的行动,因为无论他做什么,你都应该采取相同的策略。
理性的悲剧:囚徒困境的启示
如果说纳什均衡有一个 “形象代言人”,那非 囚徒困境 莫属。这个故事以最简洁的形式,揭示了个体理性选择与集体理性结果之间 残酷的冲突。
接着我们的囚徒故事:嫌疑人A和B被隔离审讯,警察开出条件:
- 都沉默:因证据不足,两人各判1年。
- 都坦白:证据确凿,两人各判5年。
- 你坦白,他沉默:你获释(0年),他重判10年。
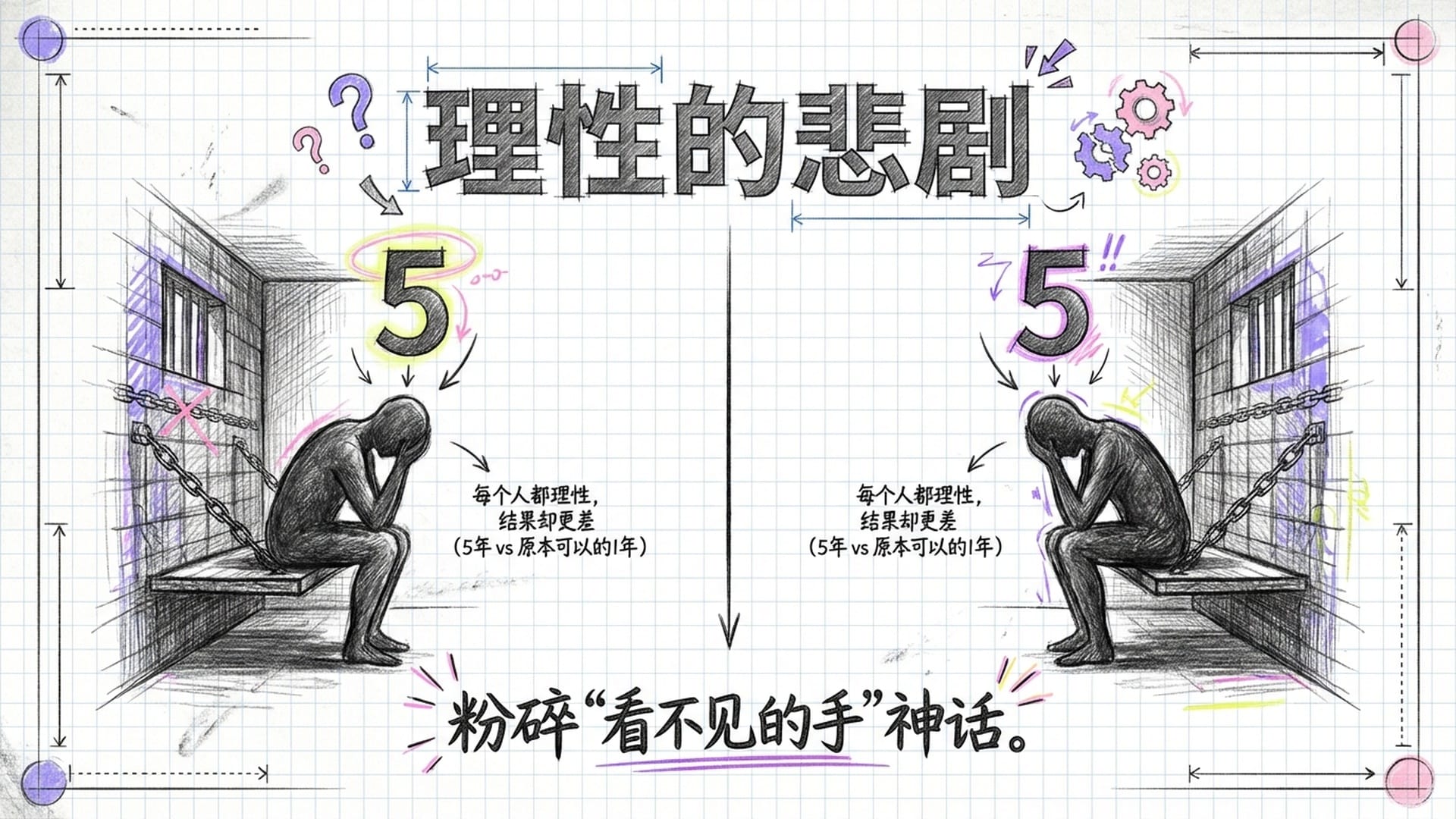
还记得我们刚才的“划线法”吗?结论是:无论对方如何选择,对个体而言,最有利的都是 “坦白”。所以,两个理性的囚徒,都会义无反顾地选择“坦白”。最终结果是两人都判5年。这个 (坦白,坦白) 的组合,便是一个 稳固的纳什均衡。
那么,这有何震撼之处?
最震撼的地方在于,回顾收益矩阵的左上角,如果两人都选择“沉默”,结果是两人都只判1年! 1年和5年,哪个更好? 对所有人都更好的是1年!
这里便出现了博弈论中最核心的 讽刺:
- 每个人都很理性:大家为了自身利益,都选择了“坦白”。
- 结果却很糟糕:这种理性的个体选择,反而导致集体陷入一个比本可以更好的局面 更差的境地。
这正是 “理性的悲剧”。它彻底颠覆了亚当·斯密的 “看不见的手” 理论——并非所有个体自私自利的行为都能自然导向社会最佳状态。在许多情况下,事实恰恰相反。
从冷战到商战:囚徒困境的现实投影
囚徒困境之所以如此重要,因为它几乎是人类社会无数冲突的 缩影,无处不在。
- 军备竞赛:冷战时期,美苏两国都面临选择:是继续扩充核武器,还是共同裁减?如果双方都裁减,人类更安全,军费也节省了。然而,谁都不敢率先裁减,担忧对方不裁减而占据优势。最终,两国投入 天文数字 的军费,制造了足以毁灭地球的武器。安全感是否提升了?没有!这便是一个 巨大的囚徒困境纳什均衡。
- 价格战:两家电商巨头拼命打价格战,你降我降,利润薄如刀片。可谁又敢率先提价呢?谁提价,谁就可能失去市场份额。最终,消费者或许高兴了,但这两大巨头却被困在一个 低利润的纳什均衡 中,无法自拔。
- 环境保护:全球变暖背景下,每个国家都知道减排的重要性,但减排需要付出 经济代价。如果他国减排而我不减排,岂不是既享受了清洁环境,又保持了经济高速增长,岂不两全其美?当每个国家都打着这种 “搭便车” 的小算盘时,结果便是全球排放失控,所有人共同承受气候灾难。
如何逃离困境?重复博弈与信任的曙光
既然囚徒困境如此令人绝望,为何人类社会尚未崩溃?为何我们仍能看到国际合作、商业联盟,乃至人与人之间的信任?
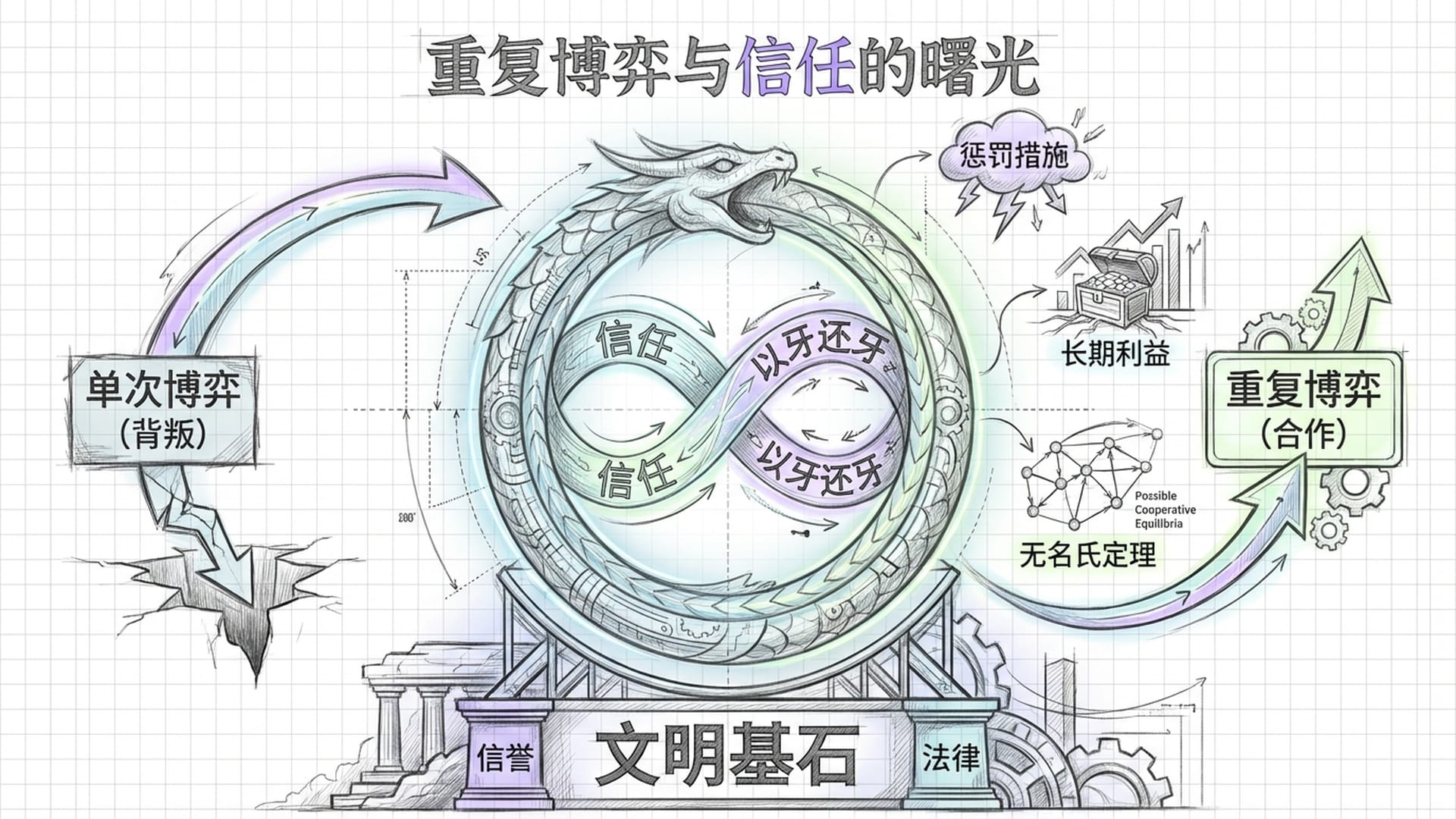
答案在于,我们大部分的博弈,并非只进行 一次。
如果囚徒困境只发生一次,结果无疑是悲剧。但如果这场游戏需要 反复进行多次,情况就截然不同了。
“我这次如果背叛了你,下次你必定会对我进行惩罚。 为了长远的利益,我们可能会选择‘以牙还牙’的策略:你对我好,我也对你好;你对我坏,我也对你坏。”
只要我们都 看重未来的收益,为了维护 长期的合作关系,我们就会愿意牺牲眼前 “背叛”的诱惑。这便是 “无名氏定理” 所阐述的:在重复博弈中,只要参与者拥有足够的耐心,合作便可以作为一种纳什均衡长期存在。
由此可见,人类社会的 道德、信誉机制、法律契约,本质上都是在将那些糟糕的“单次博弈”转化为“重复博弈”,或是通过改变博弈规则和奖励,帮助我们挣脱出那个 困境般的纳什均衡。
协调与冲突:性别战博弈的难题
如果说囚徒困境聚焦于 “是否合作” 的两难,那么 性别战 这种博弈,则着眼于 “如何合作” 的困境。这里不存在背叛,仅仅是双方对合作方式存在 不同偏好。
故事很简单:一对夫妻周五晚上约会,丈夫偏爱拳击,妻子钟情芭蕾。然而,核心在于:他们都深爱对方,宁愿陪伴对方看自己不喜欢的节目,也绝不愿 分开行动。若分开,收益便为零。
收益矩阵如下:
| 丈夫 \ 妻子 | 芭蕾 (Ballet) | 拳击 (Fight) |
|---|---|---|
| 芭蕾 | 1, 2 | 0, 0 |
| 拳击 | 0, 0 | 2, 1 |
(注:第一个数字是丈夫收益,第二个是妻子收益。数字越大越好。(1,2)表示丈夫迁就妻子看芭蕾得1分,妻子看喜欢的芭蕾得2分。)
使用“划线法”分析,你会发现这里 没有占优策略。丈夫是否选择拳击,完全取决于妻子;妻子是否选择芭蕾,同样完全取决于丈夫。
而且,你会发现存在 两个纳什均衡:
(芭蕾,芭蕾):丈夫陪妻子看芭蕾,妻子也看芭蕾。双方都在芭蕾舞剧院,谁也不想单方面改变(因为一改变就落单,收益变为0)。(拳击,拳击):妻子陪丈夫看拳击,丈夫也看拳击。双方都在拳击赛场,同样无人想单方面改变。
问题出现了!既然存在 两个纳什均衡,那最终会发生哪一个呢?纳什均衡理论并未给出明确答案。如果夫妻二人都认为对方会迁就自己,结果可能就是:丈夫去了拳击场,妻子去了芭蕾舞剧院。两人都错过了,收益是 (0,0),这是 最糟糕的结局。
性别战博弈揭示了一个深刻的道理:合作不仅是关于 是否共同行动,更在于 协调——即共同做哪件事,以及 分配——谁为此做出妥协。我们的日常生活中,公司会议确定方向、朋友聚餐选择餐厅,乃至国家间制定标准,都面临这种 “性别战”的尴尬。
如何解决? 诺贝尔奖得主谢林 提出了 “聚点” 的概念。如果某个均衡,因为文化、习惯或特定理由,在人们心中显得 更为突出,大家便会不约而同地选择它。例如,如果今天是妻子的生日,那么毫无疑问,“芭蕾舞”便是聚点。
强弱与不对称:智猪博弈的智慧
并非所有博弈的参与者都 势均力敌。有时,存在强者,也存在弱者。当这种强弱对比尤为明显时,纳什均衡会呈现出 极为有趣的样貌。这便是 智猪博弈。
故事发生在一个猪圈里。一头大猪,一头小猪。猪圈较长,一端是食槽,另一端是控制食物的按钮。
- 按钮一按,会掉出10份食物。
- 按下按钮需要消耗2份体力。
- 按下按钮的猪需要跑到食槽边吃食,而未按的猪则可在食槽边大快朵颐。
我们来分析四种情况:
- 小猪按,大猪等:小猪跑过去,大猪已将10份食物全部吃光。小猪得0份食物 - 2份体力 = -2。大猪则白得10份。
- 大猪按,小猪等:大猪跑过去,小猪因嘴小胃口小,只能吃掉6份。剩下4份归大猪。大猪得4份食物 - 2份体力 = 2。小猪白得6份。
- 都按:两头猪都跑,小猪动作慢,吃3份。大猪吃7份。小猪得3-2=1。大猪得7-2=5。
- 都不按:两头猪都饿肚子,收益都为0。
博弈分析:
我们首先从小猪的角度考虑:
- 如果大猪去按,小猪选择“等”能得6份,选择“按”只能得1份。显然,“等”更划算!
- 如果大猪不按,小猪选择“等”得0份,选择“按”得-2份(白费力气)。显然,“等”仍然划算!
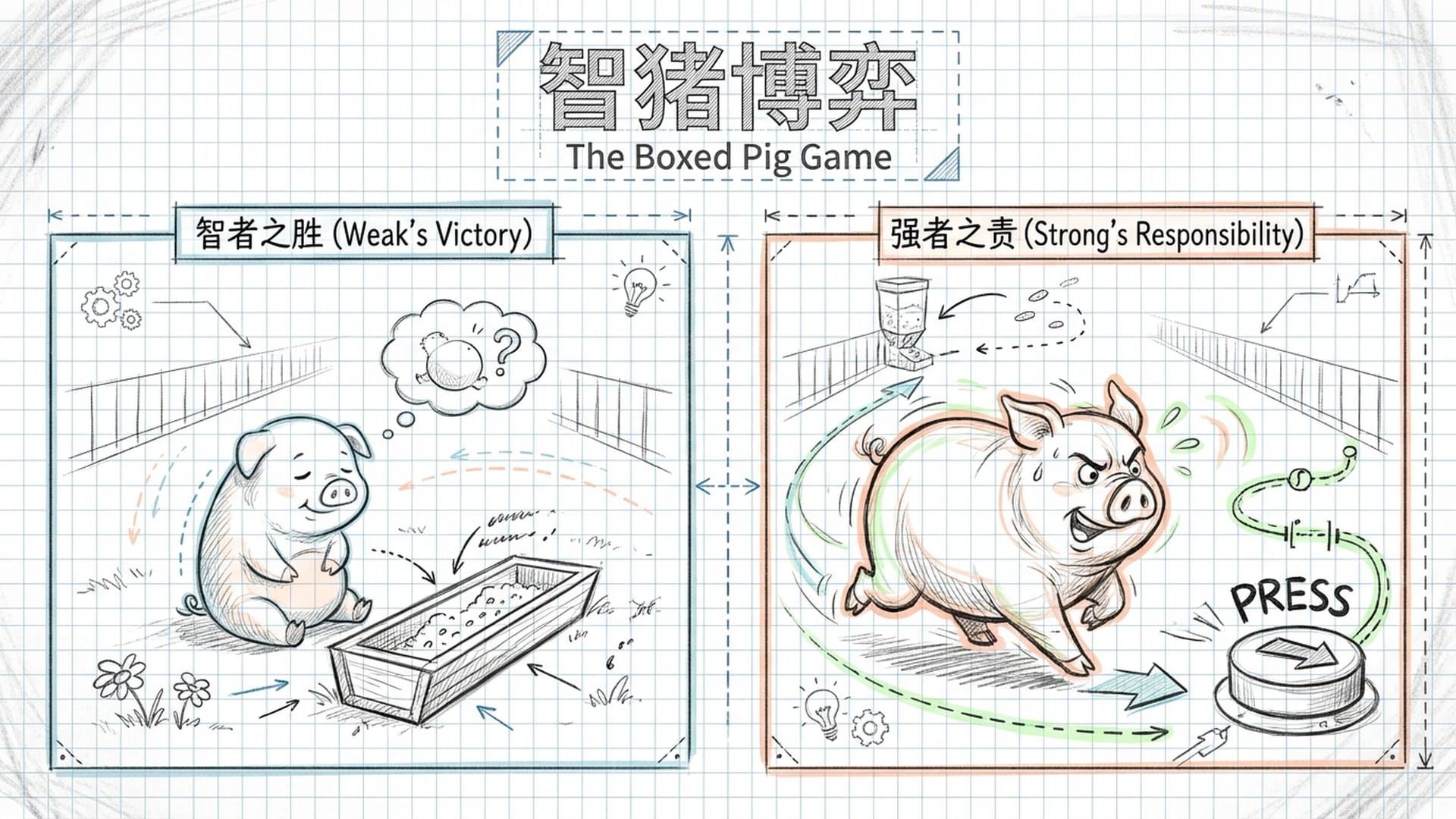
结论:无论大猪采取何种行动,“等待”都是小猪的 严格占优策略。它无需思索,只需等待即可。
接着,我们从大猪的角度考虑:大猪是聪明的,它深知小猪必然会“等待”。
那么,在大猪“知道小猪肯定会等待”的前提下,大猪只有两个选择:
- 自己去按:能获得2份收益(4份食物 - 2份体力)。
- 自己不按:大家都没食物吃,收益都为0。
为了不饿死,大猪只能选择 “自己去按”。
最终的纳什均衡便是:(大猪按,小猪等待)。
弱者的胜利与强者的责任
这个博弈结果是否 反直觉?弱小到几乎可以忽略不计的小猪,什么都没做,却白白吃掉了6份猪食。而辛辛苦苦跑路的大猪,却只获得了2份。这说明什么?
在特定的博弈结构中,弱小反倒可以成为一种 优势,而强大,则可能意味着你常常不得不承担 更多的责任。
这解释了现实世界中的许多现象:
- 大企业与小企业的创新:大公司如同大猪,有实力投入研发。而小公司呢?它可能选择 “搭便车”,等待大公司研发出技术后,再进行模仿。因为即使小公司自主研发,一旦被大公司模仿,也很难收回成本。
- 股市中的散户:大股东(大猪)会投入资金进行调研,监督管理层,因为公司治理良好,股价上涨,其收益巨大。而散户(小猪)呢?持股少,监督成本极高,收益微薄,因此理性的散户会选择 “搭便车”,不操心,坐享大股东努力带来的股价上涨。
不确定性的艺术:混合策略均衡与直觉的陷阱
我们之前讨论的,都是 纯粹策略 的博弈,例如石头剪刀布。但在许多真实的对抗中,尤其是在 零和博弈 中,如果你让对手完全摸清你的底牌,预测你的下一步,你就注定失败。为了保持 不可预测性,你需要引入 随机性。
最简单的例子是 猜硬币游戏:两人各拿一枚硬币,同时亮出,同面你赢,不同面我赢。如果我总是出正面,你就会总是出反面来赢我;如果我总是出反面,你就会总是出正面来赢我。在这个游戏中,根本不存在 纯策略的纳什均衡,因为总有一方会试图改变策略。
这时,纳什提出了 混合策略!什么是混合策略?它不是选择一个确定的行动,而是选择一个 概率分布。例如,我50%的概率出正面,50%的概率出反面。纳什证明,只要是 有限博弈,即使没有纯策略均衡,也 必定存在混合策略均衡。
计算混合均衡:无差异原理
混合策略均衡的计算,巧妙地运用了 无差异原理:
我的混合策略,必须让对手觉得,无论他采取哪个纯策略来应对,他获得的收益都 一样。只有这样,他才无法通过针对我的某个特定行动来获利,均衡才能维持。
以 足球点球大战 为例。射手可以选择射左或射右,门将可以选择扑左或扑右。
假设射手是右脚球员,射右边(强侧)进球率高,射左边(弱侧)进球率稍低。门将也有其偏好。如果射手总是射右,门将就会总是扑右。射手必须改变策略。这说明 纯策略行不通。
那么,射手应该以多大的概率射向左边、射向右边?门将又该以多大的概率扑向左边或右边呢?
根据“无差异原理”:
- 射手的混合策略,要让门将无论扑左还是扑右,他的 “期望扑救成功率”都是一样的。门将猜不透,所以他会随机扑救。
- 门将的混合策略,要让射手无论射门到左边还是右边,他的 “期望进球率”都是一样的。射手猜不透,所以他会随机射门。
经过复杂的计算(这里我们跳过数学公式),你可能会发现,为了平衡双方的能力并使对方无法选择,均衡结果可能是:门将更多地扑向射手擅长的一侧,而射手,也更多地射向他擅长的一侧。
最 反直觉 的一点是:如果你提升了自己的能力(例如射手苦练左脚,提高射左成功率),你会发现,主要改变的并非你自己的策略,而是你 对手的策略。为了应对你变强,你的对手会改变他的混合策略,而你,反而可能无需大幅改变自己的策略。这种现象在职业足球比赛中得到大量验证。顶级球员在点球时射门方向的随机性,以及门将扑救方向的随机性,都高度符合纳什混合策略均衡的预测。
直觉的陷阱:布雷斯悖论
我们通常认为,为系统增加资源总是一件好事,比如修建更多道路,增加更多网络带宽。然而纳什均衡却告诉我们,在一个由许多 自私自利个体 组成的系统中,情况可能恰恰相反——这就是著名的 布雷斯悖论。
想象一个从S点到E点的城市交通网络,有4000辆车需要通行。初始情况下,有两条路,路上存在堵车路段,车越多速度越慢。司机们会选择一个平衡点,例如两条路都耗时65分钟,这是一个纳什均衡。
现在,政府 好心办坏事了:在中间修建了一条捷径,一条几乎不耗时的高速公路。结果会怎样?
每个司机都会想:哇,有捷径了!我走捷径肯定更快!于是,所有司机都蜂拥而上涌向了这条捷径。结果出人意料:总耗时从65分钟,一下飙升到80分钟!
而且,这个80分钟的路线,也是一个 纳什均衡!因为任何一个司机想单方面换回老路,他会发现自己将花费更多时间。所以,大家都被困在了这个 更糟糕的80分钟均衡 中。
布雷斯悖论揭示了一个残酷的事实:在 缺乏宏观协调的自私系统 中,个体理性的加剧,往往会导致 集体效率的下降。修越多的路,反而可能让路更堵。
这个悖论在现实中屡见不鲜:
- 首尔拆高架:韩国首尔在拆除市中心一条高架桥后,市中心的交通拥堵反而奇迹般地缓解了。这正是因为减少了道路,反而迫使司机分散选择,找到了 更优的整体均衡。
- 体育比赛中的“尤因理论”:有时,一支球队的核心巨星缺阵,球队反而表现更好。原因在于巨星在场时,所有队友都倾向于将球传给他,让他包办一切。这就像所有车辆都涌向一条“捷径”,反而使得整个进攻线路变得单一,更容易被防守。巨星不在,球权分散,大家反而打得更活。

经济战场的硝烟:古诺与伯特兰竞争
在商业世界中,企业间的竞争便是博弈论最直接的应用。根据企业是选择 固定产量 还是 固定价格,形成了两种经典的纳什均衡模型:古诺竞争 和 伯特兰竞争。
古诺竞争:产量的博弈
假设有两家企业生产 完全相同的产品,例如矿泉水。它们同时决定各自的产量。市场上的总产量决定了产品的价格。
在古诺均衡中,每家企业都决定了一个产量,这个产量是对竞争对手产量的 “最佳回应”。结果是:双方的总产量会比一家垄断企业高,但双方的利润都还说得过去。
这解释了 OPEC(石油输出国组织) 这样的卡特尔组织。他们深知,所有成员国共同减产,可以赚取最大利润。然而,每个成员国都存在 “多生产一点” 以获取更多利润的冲动。最终结果呢?总产量往往会高于他们约定的水平,价格也因此低于垄断时期。这就是一个 古诺纳什均衡。
伯特兰竞争:价格的深渊
同样是两家企业销售 同质产品,但这次它们竞争的是 价格。消费者是完全理性的,只购买最便宜的产品。
想象一下:你定价10元,我定价9.9元,我便能抢走所有顾客。你必然不甘示弱,降价到9.8元。我又降到9.7元……这场价格战将 持续进行,直到价格降至 边际成本!也就是说,恰好能保本的最低价格。再降价就会亏损。
结果是惊人的:只要存在两家公司竞争,纳什均衡就会导致 价格等于边际成本,所有参与者的利润都变为 零!这与无数家公司充分竞争的结果如出一辙。
“伯特兰悖论” 警示我们,产品同质化严重的行业(例如航空公司、大宗商品),为何会陷入 惨烈的价格战泥潭。要摆脱这个深渊,企业必须设法:
- 产品差异化:避免销售同质化产品,通过 品牌、设计、服务 来吸引消费者,使其不仅仅依赖价格做选择。
- 合谋:尽管违法,但企业有动机 私下串通,共同抬高价格。
- 增加搜索成本:让消费者难以直接比较价格,例如通过复杂的手机套餐。
豪泰林模型:为何麦当劳总开在肯德基旁边?
伯特兰模型还有一个变体:豪泰林空间竞争模型。想象一条店铺林立的大街。两家商店选址,为了争夺最多的顾客(假设顾客只会选择最近的商店),两家店会不断向街道的 中间移动,最终挤在最中央。
这解释了为什么 同类型商店总是开得很近。它也解释了政治中的 “中值选民定理”:为了争取中间派选民,左派和右派的政党纲领,往往会变得 越来越接近、越来越相似,就像麦当劳和肯德基总是开在一起一样。
纳什均衡的局限与超越:更广阔的视野
纳什均衡虽然强大,但它并非万能灵药。在应用它时,我们必须清醒地认识到其 局限性。
纳什均衡 vs 帕累托最优:效率的缺失
从囚徒困境到布雷斯悖论,我们已经看到,纳什均衡关注的是 “大家都不后悔” 这种个体理性下的稳定,而 帕累托最优 则关注的是 “在不伤害任何人的前提下,没有人能够让自己的情况变得更好” 这种集体福利下的效率。
这两者往往是 不重合的。因此,我们看到的许多制度设计,例如 反垄断法、交通法规、环保公约,本质上都是在 “修补纳什均衡”。它们通过改变博弈规则,将那些糟糕的、低效的纳什均衡,强行推向一个对所有人来说都 更好的帕累托最优状态。
动态博弈与不可置信的威胁
纳什均衡主要处理的是 “同时出招” 的博弈。但在生活中,许多博弈是 “你先出招,我再出招” 的动态博弈。
例如,一家创业公司想进入市场。垄断巨头威胁:“你胆敢进入,我就和你打价格战,咱们同归于尽!”这个威胁听起来很吓人,但仔细想想,如果创业公司真的进入了,垄断巨头真的会 自杀式地打价格战,让彼此都亏得血本无归吗?如果它真是理性的,它可能更愿意选择 “默许并共存”。因此,这种“同归于尽”的威胁,是一种 “不可置信的威胁”。
为了剔除这种不理性的威胁,德国经济学家 泽尔腾 引入了 “子博弈精炼纳什均衡”。简单来说,就是我们从博弈的最后一步倒推回去,只保留那些在每一步都 真正符合理性 的策略。这样,那些“吓唬人”的空话,就会被排除掉。
进化博弈论:不需要“理性”的均衡
纳什均衡假设我们都是 绝对理性 的“计算机器”。但动物、微生物,甚至我们人类,很多时候并非如此。
进化博弈论 指出,均衡不一定需要高度的智能计算才能产生,它完全可以通过 自然选择,“进化”出来。
例如,在动物世界中,如果某种策略(如:对抢地盘的敌人表现怯懦)比另一种策略(如:总是表现凶狠)更容易让这种动物生存繁衍,那么这种“怯懦”的策略可能就会在种群中扩散。最终,这种稳定的种群状态,就是 “进化稳定策略”,它通常也是纳什均衡的一个精炼子集。这解释了为什么即使没有大脑的细菌,它们的行为模式也往往符合纳什均衡的预测。
结语:在博弈中寻找智慧
纳什均衡,虽然诞生于数学手稿,但早已超越了象牙塔,成为了我们理解这个 复杂世界的通用语言。
它像一面镜子,映照出人类理性的 光辉与局限。它告诉我们,在这个相互紧密连接的世界里,每个人的命运不仅取决于自身的奋斗,更取决于你与他人 互动的结构。
它让我们警惕 “理性的自负”:个体最优,不等于集体最优。自由放任,往往并非最佳结果。 它教导我们 换位思考:理解对手的视角,不只是一种美德,更是一种生存必备的战略能力。 它指引我们 制度设计:好的制度,应能将那个“纳什均衡点”尽可能地推向“帕累托最优点”,让每个人在追求私利的同时,也能 不经意间为集体做出贡献。
从冷战的核威慑平衡,到互联网平台上的竞争规则,再到你我日常生活中与家人、朋友、同事之间的各种人际博弈, 纳什均衡无处不在。掌握这一思维工具,你就拥有了一双能够看穿社会现象背后 隐形逻辑的慧眼。真正的智慧,不只是知道如何做出最好的选择,更是懂得如何在众人纷繁的选择和算计中,找到那个 微妙、关键,甚至带有一丝无奈的平衡点。
 |  |  |
